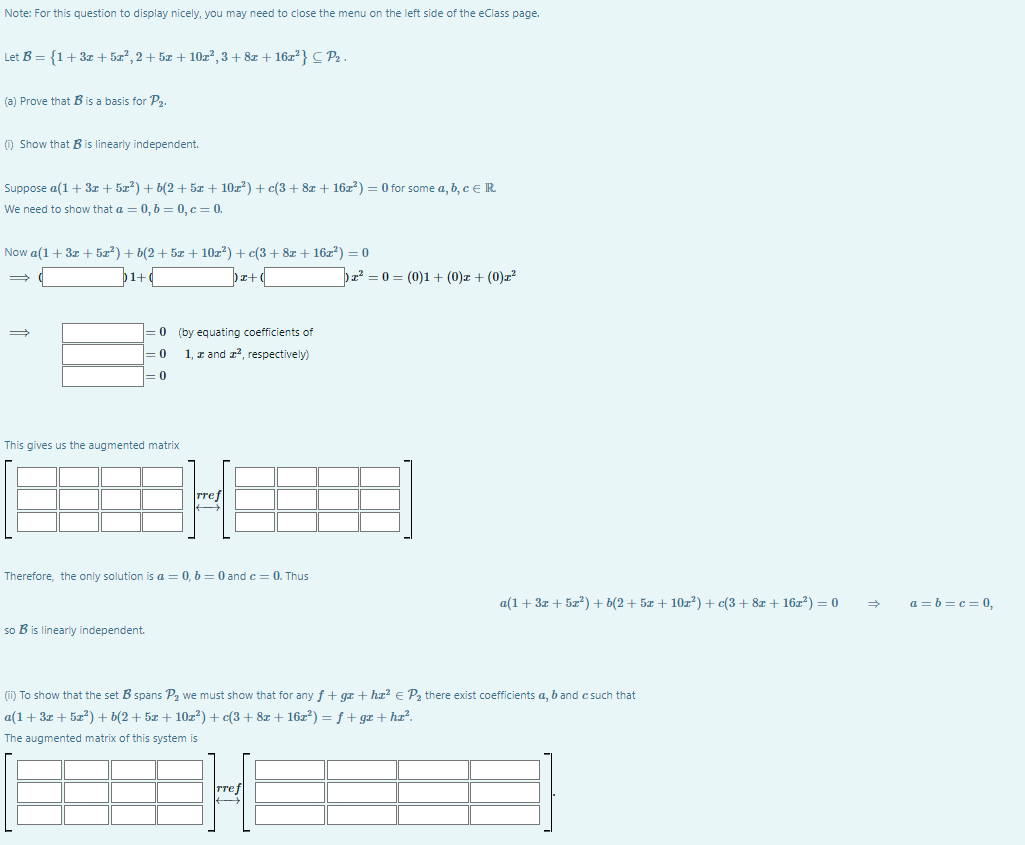
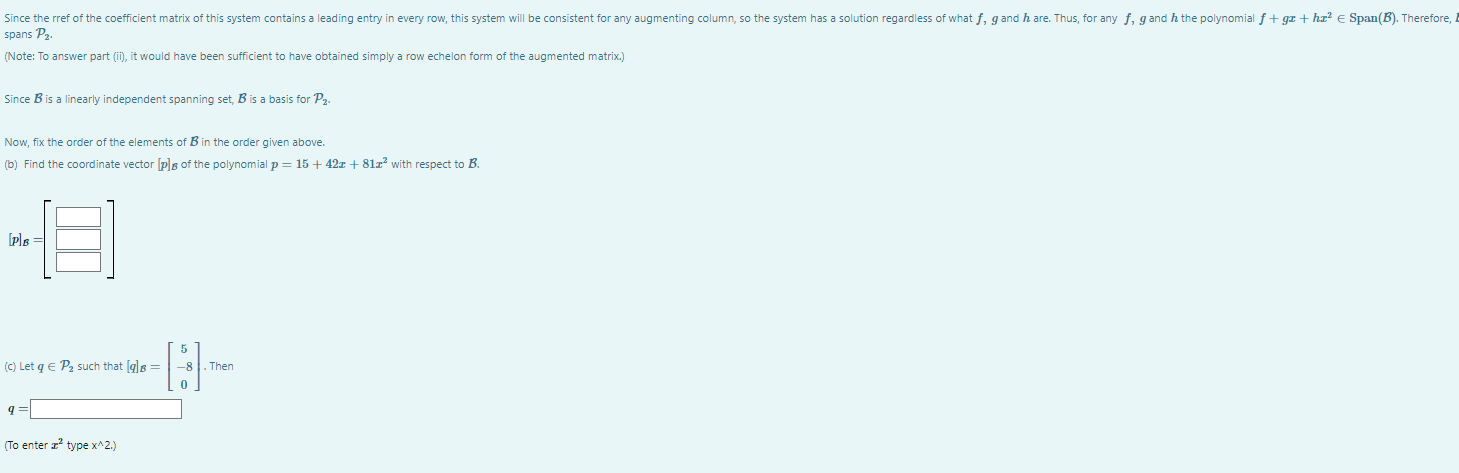
Note: For this question to display nicely, you may need to close the menu on the left side of the eClass page. Let B = {1 + 3x + 513, 2 + 5x + 1013, 3 + 81 + 161}} CP2 . (a) Prove that B is a basis for P2. (@) Show that B is linearly independent. Suppose a(1 + 3: + 527) + b(2 + 5x + 10r?) + c(3 + 8x + 161?) = 0 for some a, b, ce IR We need to show that a = 0, b = 0, c = 0. Now a(1 + 3x + 51?) + b(2 + 52 + 10r?) + c(3 + 8 + 16:?) =0 p1+q 12 = 0 = (0)1 + (0)r + (0)13 = 0 (by equating coefficients of =0 1, x and 12, respectively) = 0 This gives us the augmented matrix Tej E Therefore, the only solution is a = 0, b = 0 and c = 0. Thus a(1 + 3x + 5x2) + 6(2 + 5: + 10r?) + c(3 + 8: + 16z?) = 0 a=b= c =0, so B is linearly independent. (i) To show that the set B spans Pa we must show that for any f + gr + he?