Note:- please send me answer in typed form strictly prohibited hand written solution please don't use chatgpt otherwise I will report coursehero

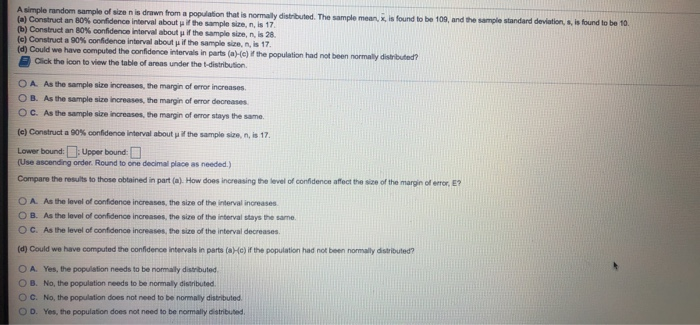
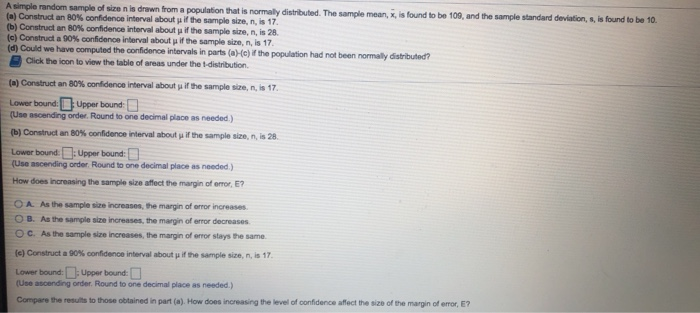
A simple random sample of size n is drawn from a population that is normally distributed. The sample mean, x, is found to be 109, and the sample standard deviation, s, is found to be 10. [a] Construct an 80%) confidence interval about p if the sample size, n, is 17. [b) Construct an 80%% confidence Interval about p if the sample size, n, Is 28. [c) Construct a 90% confidence interval about p if the sample size, n, is 17. [d) Could we have computed the confidence intervals in parts (a)-(c) if the population had not been normaly disin Click the icon to view the table of areas under the t-distribution. Q A. As the sample size increases, the margin of error increases. O B. As the sample size increases, the margin of error doorcauses. O C. As the sample size increases, the margin of error stays the same. [e) Construct a 90% confidence Interval about p if the sample size, n, is 17. Lower bound: :Upper bound: (Use ascending order. Round to one decimal place as needed.) Compare the results to those obtained in part (a]. How does increasing the level of confidence affect the size of the marg O A. As the lovol of confidence increases, the size of the interval increases. O B. As the level of confidence increases, the size of the interval stays the same. O C. As the level of confidence increases, the size of the interval decreases. (d) Could we have computed the confidence intervals in parts (a)-(c) if the population had not been normally distributed? Q A. Yes, the population needs to be normally distributed O B. No, the population needs to be normally distributed. () C. No, the population does not need to be normaly distributed. O D. Yes, the population does not need to be normally distributedA simple random sample of size n is drawn from a population that is normally distributed. The sample mean, x, is found to be 109, and the sample standard deviation, s, is found to be 10. (a) Construct an 80% confidence interval about us if the sample size, n, is 17. (b) Construct an 80% confidence intorval about p if the sample size, n, is 28. (c) Construct a 90% confidence interval about p if the sample size, n, Is 17. (d) Could we have computed the confidence intervals in parts (a)-(e) if the population had not been normally distributed? Click the icon to view the table of areas under the 1-distribution. (a] Construct an 80% confidence interval about p if the sample size, n, is 17. Lower bound: | : Upper bound (Use ascending order, Round to one decimal place as needed.) (b) Construct an 80%% confidence interval about p if the sample size, n, is 28, Lower bound: : Upper bound: (Use ascending order, Round to one decimal place as needed.) How does increasing the sample size affect the margin of ones, E7 O A. As the sample size increases, the margin of orfor increases. O B. As the sample size increases, the margin of error decreases. O C. As the sample size increases, the margin of oror slays the same. (e] Construct a 90%% confidence interval about p if the sample size, n, is 17. Lower bound: : Upper bound (Use ascending order, Round to one decimal place as needed.) Compare the results to those obtained in part (a). How does increasing the level of confidence affect the size of the margin of eror, ET