NOTE: please solve it quickly
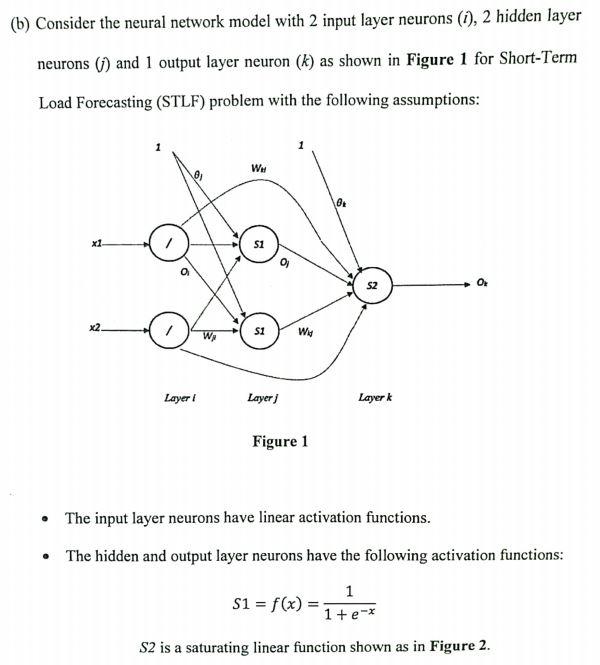
(b) Consider the neural network model with 2 input layer neurons (1), 2 hidden layer neurons () and 1 output layer neuron (k) as shown in Figure 1 for Short-Term Load Forecasting (STLF) problem with the following assumptions: WH 8 S1 $2 0 x2 S1 W Wy Layer 1 Layer Layer Figure 1 . The input layer neurons have linear activation functions. The hidden and output layer neurons have the following activation functions: 1 S1 = f(x) = 1+ e* S2 is a saturating linear function shown as in Figure 2. +1 450 nete -1 Figure 2 . Use the following standard convention: Input to neuron j: net; and input to neuron k: nete o learning rate: 7, momentum rate: and target: Tk i) ii) Derive an equation for the output of the neural network based on the inputs Xi and the rest of the parameters. If all the current weights have very similar values, and suddenly the neural network experiences a large negative input, describe by using the mathematical proof what would happen to the neural network output, Ok Based on the following generalized delta rule (GDR) and formulas, derive the adaptation algorithm of the weights between the output and hidden layer neurons (AWx)) and the weights between the output and the input iii) layer neurons (AWki) (*Note: For the derivation, consider the linear part of S2 only) GDR: AWnew = 980 + AWold where is the error signal. And the neural network error E as: 1 E = 2 (Tie Ox)? CTE where Tk is the target signal and Ok is the output of neural network. [Use Y_ where necessary] Next, derive the adaptation algorithm for the weights between the hidden and input layer neurons: AWji. (b) Consider the neural network model with 2 input layer neurons (1), 2 hidden layer neurons () and 1 output layer neuron (k) as shown in Figure 1 for Short-Term Load Forecasting (STLF) problem with the following assumptions: WH 8 S1 $2 0 x2 S1 W Wy Layer 1 Layer Layer Figure 1 . The input layer neurons have linear activation functions. The hidden and output layer neurons have the following activation functions: 1 S1 = f(x) = 1+ e* S2 is a saturating linear function shown as in Figure 2. +1 450 nete -1 Figure 2 . Use the following standard convention: Input to neuron j: net; and input to neuron k: nete o learning rate: 7, momentum rate: and target: Tk i) ii) Derive an equation for the output of the neural network based on the inputs Xi and the rest of the parameters. If all the current weights have very similar values, and suddenly the neural network experiences a large negative input, describe by using the mathematical proof what would happen to the neural network output, Ok Based on the following generalized delta rule (GDR) and formulas, derive the adaptation algorithm of the weights between the output and hidden layer neurons (AWx)) and the weights between the output and the input iii) layer neurons (AWki) (*Note: For the derivation, consider the linear part of S2 only) GDR: AWnew = 980 + AWold where is the error signal. And the neural network error E as: 1 E = 2 (Tie Ox)? CTE where Tk is the target signal and Ok is the output of neural network. [Use Y_ where necessary] Next, derive the adaptation algorithm for the weights between the hidden and input layer neurons: AWji
