Note: Program Language is C

64 bit, 2's complement representation, signed integer representation for INT_MAX and INT_MIN

right shift operator >> is using arithmetic right shift, not logical right shift.

If possible, I would like to see intermediate steps on the binary level (0,1).

The process to final answer would be really helpful.

Final result is in Hexadecimal presentation. ex: 0xFFFFFFFFFFFFFFFF or 0x8000000000000000

Some images below might be helpful for this question:

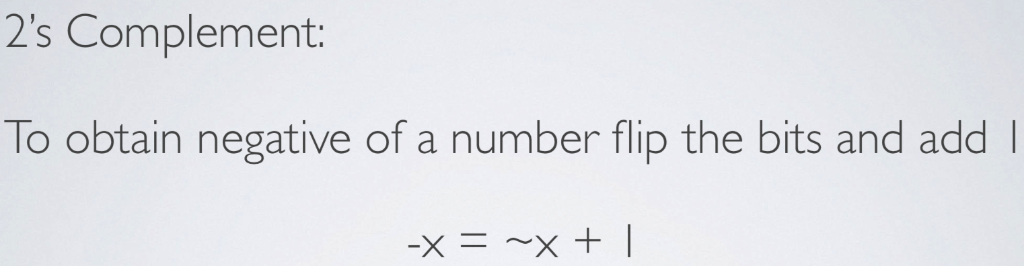
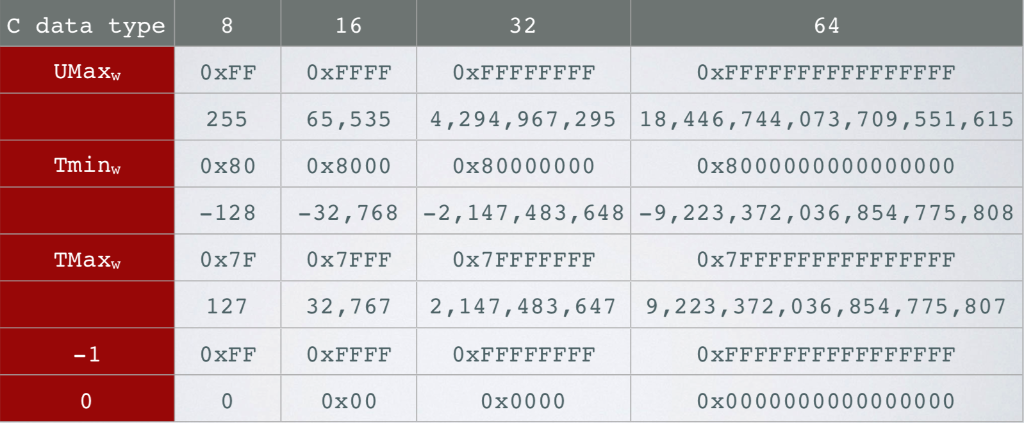
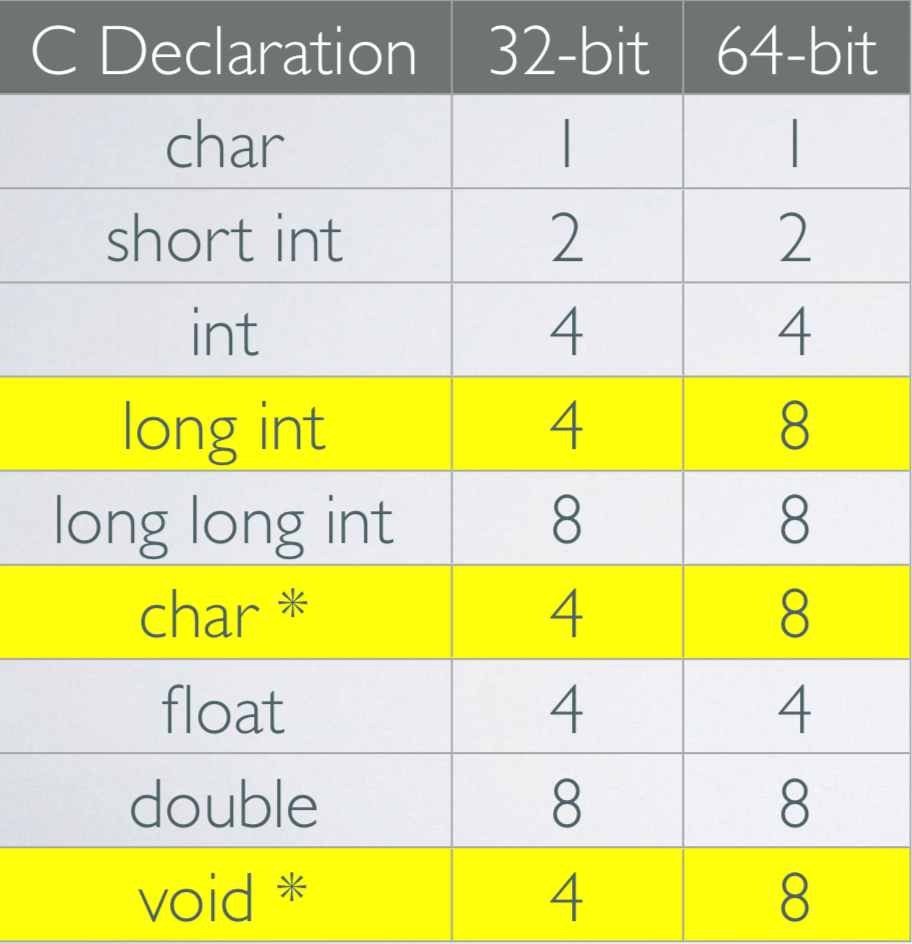
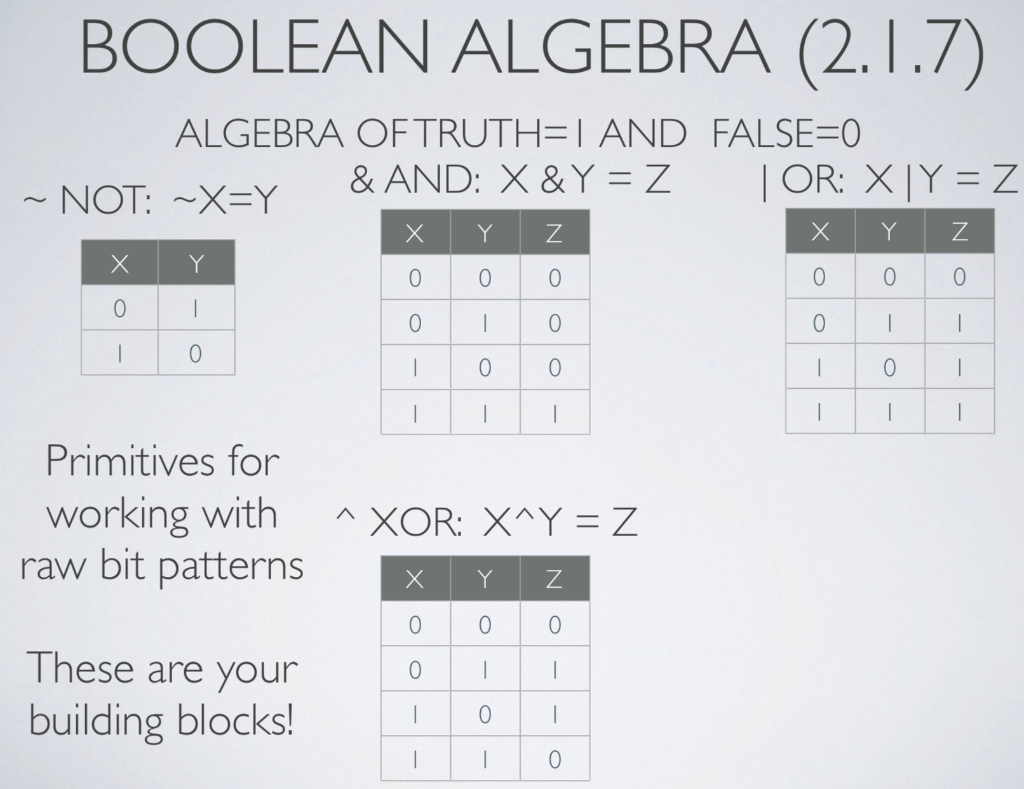
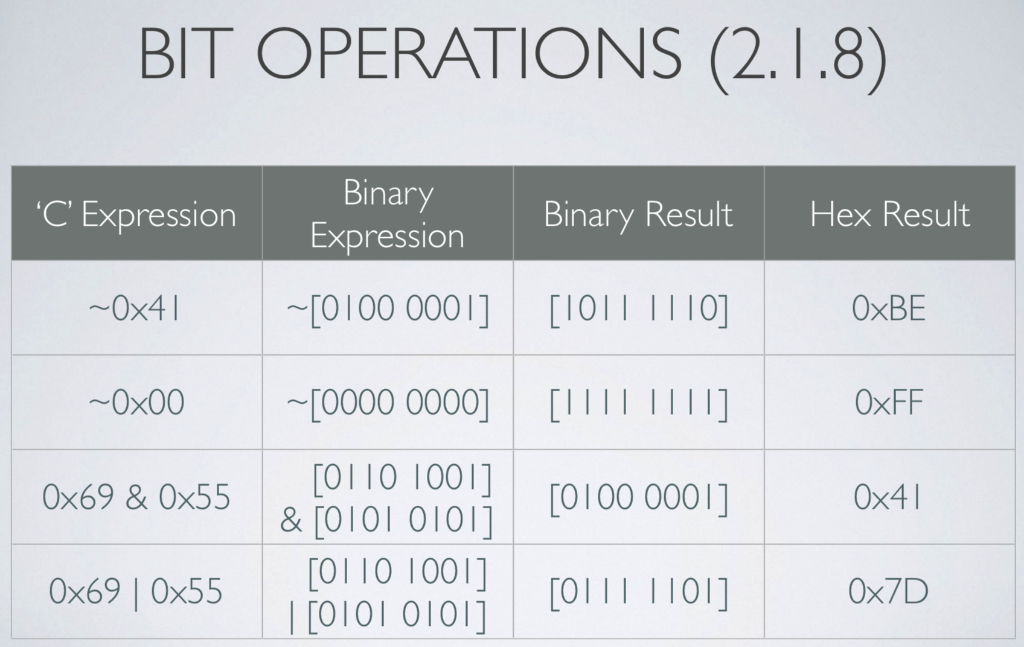
2) 2's Complement Respresentatioin Fill in the below table assuming a 64 bit computer that uses 2's complement representation, INT. and INT MIN are defined as the computer's signed integer representation maximum and minimum value respectively, and: int x = INT-MIN, y = Oxdecaf bad , z = INT-MAX, i (sizeof (char *) sizeof (int *)); = + C Expession Hexadecimal 2K 16 y16) Oxfffif ("(0x10>>21+1) ==-(1>>2) x)33 1))& y ( (y3)+INT..MIN) ^ ((yk:2 types logical and arthmetic: logical right shift: left end filled with k zeros . arithmetic right shift: left end filled with k repetitions of most significant bit. T001 0000] OI010000] T000001 T0 [0000 1001] 000001 10] II0 x>4 (logical (arithmetic) c data type 16 32 64 UMaxw 0xFF 0xFFFF 0xFFFFFFFF 255 65,535 4,294,967,295 18,446,744,073,709,551,615 0x80 0x8000 0x80000000 0xFFFFFFFFFFFFFFFF Tminw 0x8000000000000000 128 0x7F 0x7FFF 0x7FFFFFFF 127 32,767 2,147,483,647 9,223,372,036,854,775,807 0XFF 0xFFFF 32,768 -2,147,483,648-9,223,372,036,854,775,808 TMaxw 0x7FFFFFFFFFFFFFFF 0xFFFFFFFF 0xFFFFFFFFFFFFFFFF 0x00 0x0000 0x0000000000000000 C Declaration 32-bit 64-bit char short int int long int 2 4 2 4 4 long long int 8 4 char* float double void 4 4 BOOLEAN ALGEBRA (2.1.7) ALGEBRA OF TRUTH-I AND FALSE 0 NOT:X-Y X Y Z X YZ XY Primitives for working with raw bit patterns XOR: XAY - Z X Y Z These are your 0 building blocks! CTWO KINDS OF BOOLEAN OPERATIONS (2.1.8, 2.1.9) BITWISE LOGICAL 1, && operate on vector of bits TRUEX0 and 0-FALSE-X-_ 0 result is a vector of bits operates on integral types first map then apply boolean operation to produce O I Conditional evaluation BIT OPERATIONS (2.1.8) Expression Binary Result [0100 0001] [IOIT TTT0] 0x41 OxBE 0x00[0000 0000] [I 0xFF [0 110 1001] 1000001] | & [010l oi0l] 0x4l 0x69|0x55 | |[0101 0101] | 0x7D 2) 2's Complement Respresentatioin Fill in the below table assuming a 64 bit computer that uses 2's complement representation, INT. and INT MIN are defined as the computer's signed integer representation maximum and minimum value respectively, and: int x = INT-MIN, y = Oxdecaf bad , z = INT-MAX, i (sizeof (char *) sizeof (int *)); = + C Expession Hexadecimal 2K 16 y16) Oxfffif ("(0x10>>21+1) ==-(1>>2) x)33 1))& y ( (y3)+INT..MIN) ^ ((yk:2 types logical and arthmetic: logical right shift: left end filled with k zeros . arithmetic right shift: left end filled with k repetitions of most significant bit. T001 0000] OI010000] T000001 T0 [0000 1001] 000001 10] II0 x>4 (logical (arithmetic) c data type 16 32 64 UMaxw 0xFF 0xFFFF 0xFFFFFFFF 255 65,535 4,294,967,295 18,446,744,073,709,551,615 0x80 0x8000 0x80000000 0xFFFFFFFFFFFFFFFF Tminw 0x8000000000000000 128 0x7F 0x7FFF 0x7FFFFFFF 127 32,767 2,147,483,647 9,223,372,036,854,775,807 0XFF 0xFFFF 32,768 -2,147,483,648-9,223,372,036,854,775,808 TMaxw 0x7FFFFFFFFFFFFFFF 0xFFFFFFFF 0xFFFFFFFFFFFFFFFF 0x00 0x0000 0x0000000000000000 C Declaration 32-bit 64-bit char short int int long int 2 4 2 4 4 long long int 8 4 char* float double void 4 4 BOOLEAN ALGEBRA (2.1.7) ALGEBRA OF TRUTH-I AND FALSE 0 NOT:X-Y X Y Z X YZ XY Primitives for working with raw bit patterns XOR: XAY - Z X Y Z These are your 0 building blocks! CTWO KINDS OF BOOLEAN OPERATIONS (2.1.8, 2.1.9) BITWISE LOGICAL 1, && operate on vector of bits TRUEX0 and 0-FALSE-X-_ 0 result is a vector of bits operates on integral types first map then apply boolean operation to produce O I Conditional evaluation BIT OPERATIONS (2.1.8) Expression Binary Result [0100 0001] [IOIT TTT0] 0x41 OxBE 0x00[0000 0000] [I 0xFF [0 110 1001] 1000001] | & [010l oi0l] 0x4l 0x69|0x55 | |[0101 0101] | 0x7D