Note: show solution steps and ensure you have the correct answers.

Q1)

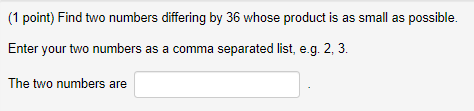
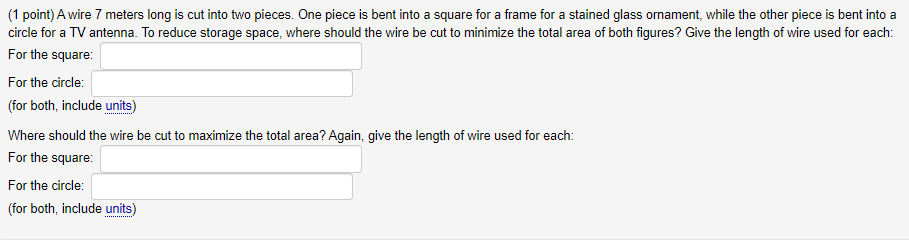
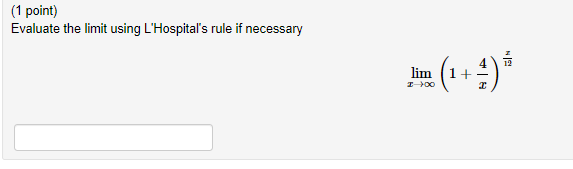
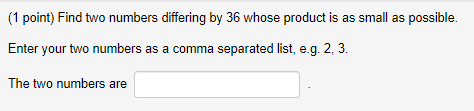
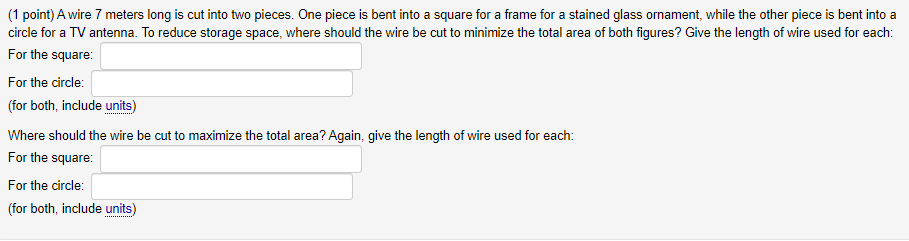
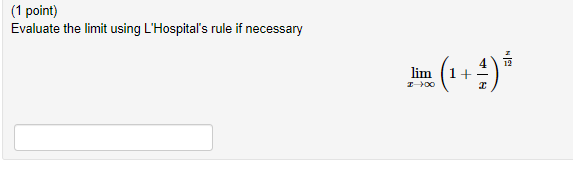
(1 point) A cylindrical can, open at the top, is to hold 520 cm of liquid. Find the height and radius that minimize the amount of material needed to manufacture the can. Enter your answer with rational exponents, and use pi to represent J. Radius= Height=Apply L'Hopital's Rule to evaluate the following limit. It may be necessary to apply it more than once. - 1 lim There - 1Find the point P on the graph of the function y = v closest to the point (4, 0) The r coordinate of P is:(1 point} Find two numbers differing by 35 whose produot is as small as possible. Enter your two numbers as a comma separated list. so. 2: 3. The two numbers are (1 point}Aience is to be built to enclose a rectangular area of 240 square feet. The fence along three sides is to be made of material that costs 4 dollars per foot: and the material for the fourth side costs 15 dollars per foot. Find the dimensions ofthe enclosure that is most economical to construct. Dimensions: 3-: 1 point} Awire T meters long is cut into two pieces. One piece is bent into a square for a frame for a stained glass ornament: while the ether piece is bent into a circle fer a TV antenna. To reduce storage space: where shculd the wire be cut to minimize the total area cf bcth gures? Give the length of wire used for each: :cr the square: For the circle: for bath: includegn'rts} Where should the wire be cm to maximize the total area? Again: give the length of wire used fcr each: :cr the square: For the circle: for bath: includeun'rts} (1 point) Evaluate the limit using L'Hospital's rule if necessary lim 1+(1 point) Compute the following limit using I'Hopital's rule if appropriate. Use INF to denote co and MINF to denote -co. lim 8 sin(r) In(x) =