Note that the decision variables can also be defined as the number of shares to invest in each stock/bond (rather than the dollar amounts). The objective function and constraints can then be modified accordingly. The trick of this problem is to define the variable R for the worse return and then add constraints 2-5 to ensure that R is the minimum return across all states.

QUESTION: what if the investor is risk taking and would like to maximise the return in the best case? And what if the investor is risk neutral who would like to maximise the expected return (provided that the probability of each state is known, say 0.25, 0.4, 0.15, 0.2)?

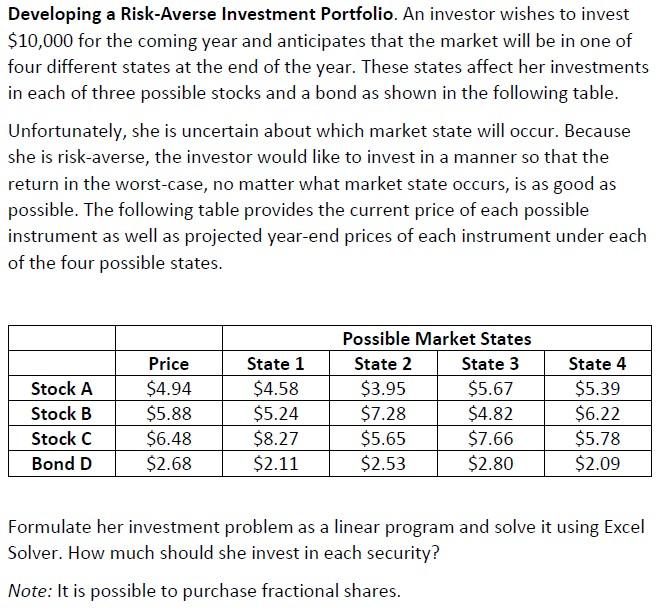
Developing a Risk-Averse Investment Portfolio. An investor wishes to invest $10,000 for the coming year and anticipates that the market will be in one of four different states at the end of the year. These states affect her investments in each of three possible stocks and a bond as shown in the following table. Unfortunately, she is uncertain about which market state will occur. Because she is risk-averse, the investor would like to invest in a manner so that the return in the worst-case, no matter what market state occurs, is as good as possible. The following table provides the current price of each possible instrument as well as projected year-end prices of each instrument under each of the four possible states. Stock A Stock B Stock C Bond D Price $4.94 $5.88 $6.48 $2.68 State 1 $4.58 $5.24 $8.27 $2.11 Possible Market States State 2 State 3 $3.95 $5.67 $7.28 $4.82 $5.65 $7.66 $2.53 $2.80 State 4 $5.39 $6.22 $5.78 $2.09 Formulate her investment problem as a linear program and solve it using Excel Solver. How much should she invest in each security? Note: It is possible to purchase fractional shares. - Let A = amount in dollars to invest stock A B = amount in dollars to invest stock B C = amount in dollars to invest stock C D = amount in dollars to invest bond D R = the minimum returned value over all states, i.e., the return in the worst scenario Max R s.t. A + B + C + D = 10000 RS 4.58*(A/4.94) + 5.24*(B/5.88) + 8.27*(C/6.48) + 2.11*(D/2.68) R$ 3.95*(A/4.94) + 7.28*(B/5.88) + 5.65*(C/6.48) + 2.53*(D/2.68) R$ 5.67*(A/4.94) + 4.82*(B/5.88) + 7.66*(C/6.48) + 2.80*(D/2.68) RS 5.39*(A/4.94) + 6.22*(B/5.88) +5.78*(C/6.48) + 2.09*(D/2.68) A, B, C, D20 Developing a Risk-Averse Investment Portfolio. An investor wishes to invest $10,000 for the coming year and anticipates that the market will be in one of four different states at the end of the year. These states affect her investments in each of three possible stocks and a bond as shown in the following table. Unfortunately, she is uncertain about which market state will occur. Because she is risk-averse, the investor would like to invest in a manner so that the return in the worst-case, no matter what market state occurs, is as good as possible. The following table provides the current price of each possible instrument as well as projected year-end prices of each instrument under each of the four possible states. Stock A Stock B Stock C Bond D Price $4.94 $5.88 $6.48 $2.68 State 1 $4.58 $5.24 $8.27 $2.11 Possible Market States State 2 State 3 $3.95 $5.67 $7.28 $4.82 $5.65 $7.66 $2.53 $2.80 State 4 $5.39 $6.22 $5.78 $2.09 Formulate her investment problem as a linear program and solve it using Excel Solver. How much should she invest in each security? Note: It is possible to purchase fractional shares. - Let A = amount in dollars to invest stock A B = amount in dollars to invest stock B C = amount in dollars to invest stock C D = amount in dollars to invest bond D R = the minimum returned value over all states, i.e., the return in the worst scenario Max R s.t. A + B + C + D = 10000 RS 4.58*(A/4.94) + 5.24*(B/5.88) + 8.27*(C/6.48) + 2.11*(D/2.68) R$ 3.95*(A/4.94) + 7.28*(B/5.88) + 5.65*(C/6.48) + 2.53*(D/2.68) R$ 5.67*(A/4.94) + 4.82*(B/5.88) + 7.66*(C/6.48) + 2.80*(D/2.68) RS 5.39*(A/4.94) + 6.22*(B/5.88) +5.78*(C/6.48) + 2.09*(D/2.68) A, B, C, D20