Question: Note: Think about the assumptions that are you making in your solution. For the questions below this usually refers to independence and all outcomes are
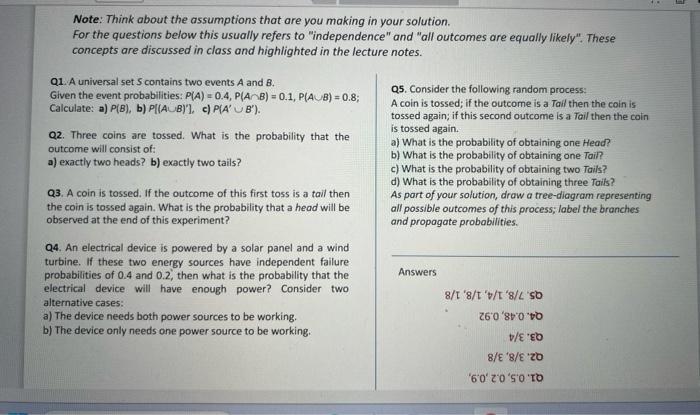
Note: Think about the assumptions that are you making in your solution. For the questions below this usually refers to "independence" and "all outcomes are equally likely". These concepts are discussed in class and highlighted in the lecture notes. Q1. A universal set S contains two events A and B. Given the event probabilities: P(A)=0.4,P(AB)=0.1,P(AB)=0.8; Calculate: a) P(B), b) P{(AB)], c) P(AB). Q2. Three coins are tossed. What is the probability that the outcome will consist of: a) exactly two heads? b) exactly two tails? Q3. A coin is tossed. If the outcome of this first toss is a tail then the coin is tossed again. What is the probability that a head will be observed at the end of this experiment? Q4. An electrical device is powered by a solar panel and a wind turbine. If these two energy sources have independent failure probabilities of 0.4 and 0.2 , then what is the probability that the electrical device will have enough power? Consider two alternative cases: a) The device needs both power sources to be working. b) The device only needs one power source to be working. Q5. Consider the following random process: A coin is tossed; if the outcome is a Tail then the coin is tossed again; if this second outcome is a Toil then the coin is tossed again. a) What is the probability of obtaining one Head? b) What is the probability of obtaining one Tain? c) What is the probability of obtaining two Tails? d) What is the probability of obtaining three Toils? As part of your solution, draw a tree-diagram representing all possible outcomes of this process; label the branches and propagate probabilities. Answers 8/8/tv/T8/Lso260800.0/O
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


