Note: This is a scheme programming language task, Please don't give answer if you don't know about anything. Please write what is asked. Write functions for the following using the scheme programming language.

Part 1:

The task for this lab is to create a function that returns another function. This function is meant to mimic the Binomial theorem (below).

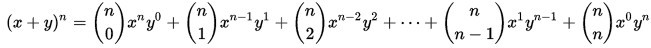
Your function, called power, should take two arguments. Its arguments will be the variables to be expanded. For example given (power x y): x and y would be the variables to be expanded. Your power function should return a function that takes two lists. These two lists will contain the exponents to which we will raise our variables. Please refer to chapter 8 to see how to write a function that returns a function.

The returned function will take two lists of numbers(list1 and list2) and return a list of lists. Each sublist in the returned list will have two lists within it:

One has the first variable, the carrot atom (^) and the power its raised to(car of list1). (x^ 2) for example. The other has the second variable, the carrot aton(^) and the power its raised to(car of list2).

An example call will look like: ((power 'x 'y) '(3 2 1 0) (reverse '(3 2 1 0))) Which should produce: '( ((x ^ 3) (y ^ 0)) ((x ^ 2) (y ^ 1)) ((x ^ 1) (y ^ 2)) ((x ^ 0) (y ^ 3)) ) Notice that X is raised to 3 while Y is raised to 0 in the first pairing.

Part II:

To complete the binomial theorem, we need to add in the coefficients to each term in the list. Create a function called coeff, which takes two lists as its arguments. The first argument should be the list produced by the function power and the second should be a list of the coefficients we want to use. You can obtain this list from a call to your Pascal function from a previous lab.

For example:

(coeff ((power 'x 'y) '(3 2 1 0) (reverse '(3 2 1 0))) '(1 3 3 1)) should produce

'((1 (x ^ 3) (y ^ 0)) (3 (x ^ 2) (y ^ 1)) (3 (x ^ 1) (y ^ 2)) (1 (x ^ 0) (y ^ 3)))

(r + y)n-( )-n3/0t. (?)-n-13/1-G)-n-23/2 + ... + n )-"-22/2 zlyn-1 +" (a)203 n-1 n (r + y)n-( )-n3/0t. (?)-n-13/1-G)-n-23/2 + ... + n )-"-22/2 zlyn-1 +" (a)203 n-1 n