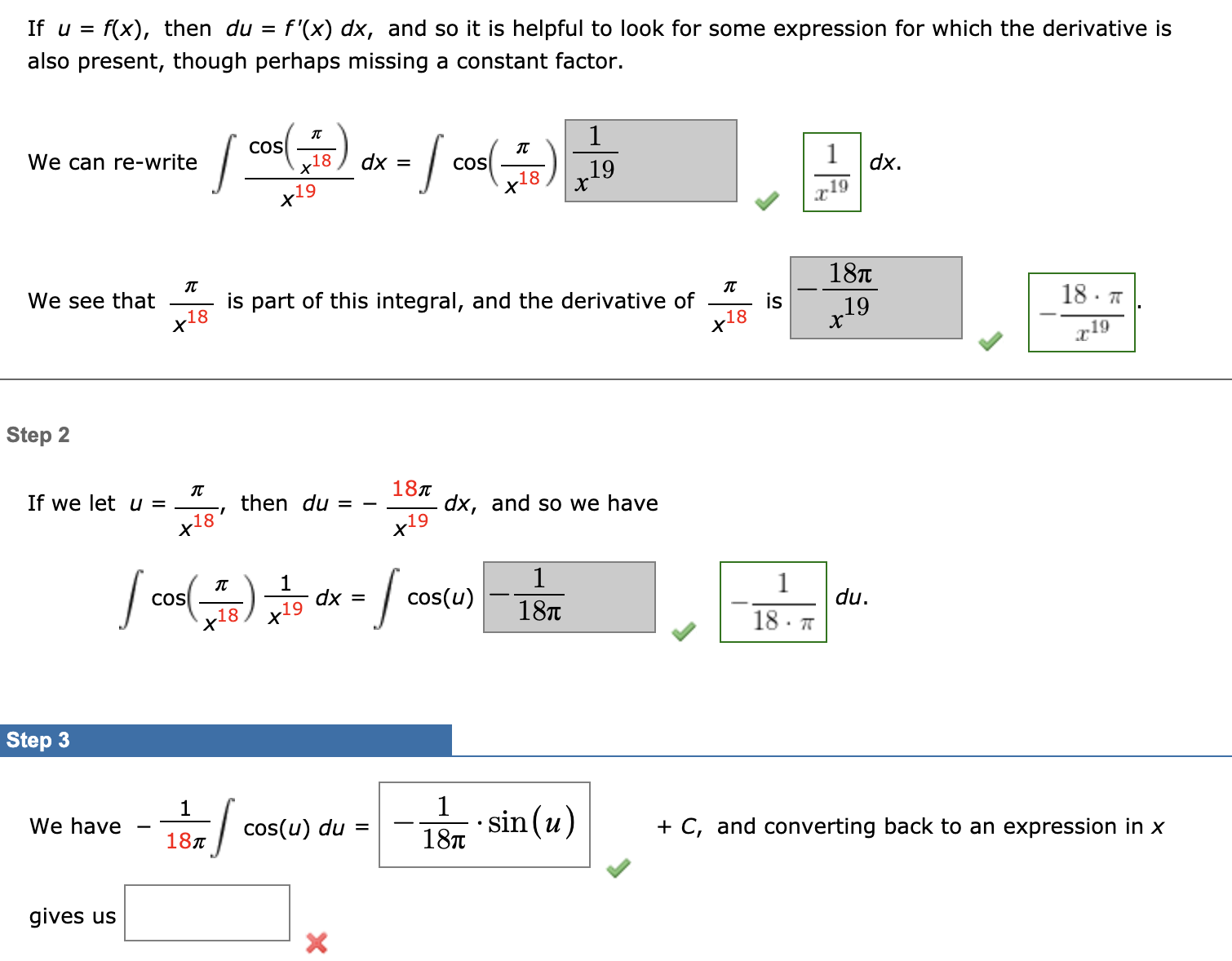
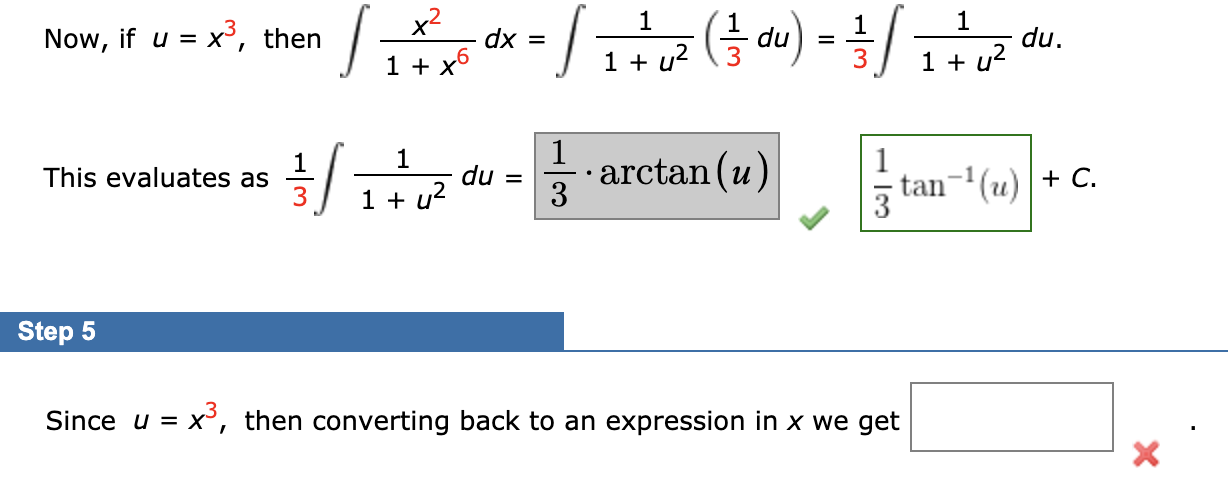
Question: Now, if u = In(x), then (In(x) ) 47 dx = X u47 du. 1 48 This evaluates as u47 du 48 u + C.
Now, if u = In(x), then (In(x) ) 47 dx = X u47 du. 1 48 This evaluates as u47 du 48 u + C. 48 Step 4 Since u = In(x), then converting back to an expression in x we get H 48 148 + C =If u = f(x), then du = f'(x) dx, and so it is helpful to look for some expression for which the derivative is also present, though perhaps missing a constant factor. We can re-write COS x 18 dx = cos X 19 dx. -19 181 We see that is part of this integral, and the derivative of is x18 19 18 . 7 y18 7-19 Step 2 If we let U = then du = - y18 x 19 dx, and so we have cos x19 dx = 1 x18 cos ( u ) 1 181 du. 18 . 7 Step 3 We have 1 cos(u) du = 1 18 . sin (u) + C, and converting back to an expression in x gives us XNow, if u = x, then 1+ x6 dx = 1 + 02 3 du 3 1 + 42 du. This evaluates as W H 1 du = 1 1 + 12 Co arctan (u) tan ' (u) + C. Step 5 Since u = x', then converting back to an expression in x we get X
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts