Question: Now prove by mathematical induction that the solution that you guessed for the sequence in previous question is correct. Solution to recursively defined sequence Given

Now prove by mathematical induction that the solution that you guessed for the sequence in previous question is correct.

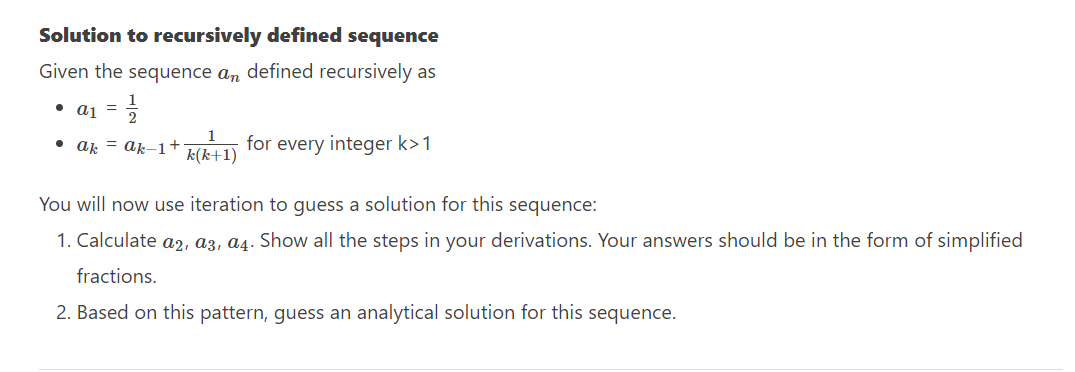
Solution to recursively defined sequence Given the sequence an defined recursively as - a1=21 - ak=ak1+k(k+1)1 for every integer k>1 You will now use iteration to guess a solution for this sequence: 1. Calculate a2,a3,a4. Show all the steps in your derivations. Your answers should be in the form of simplified fractions. 2. Based on this pattern, guess an analytical solution for this sequence. Problem Statement ( 3 marks) The conjecture that you are proving, is expressed symbolically in the form nD,P(n). - (1 mark) What is the set D ? - (2 mark) What is the predicate function P(n) in symbolic form? Base Case (2 marks) Prove your base case here Inductive Step (10 marks) a) Inductive step setup. - (2 marks) State the assumption in the inductive step and identify the inductive hypothesis. - (2 marks) State what you will be proving in the inductive step. b) Remainder of Inductive step ( 6 marks). Finish your proof here. Be sure to justify every step. particularly why the inductive hypothesis and recursive definitions can be applied

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

StepbyStep Solution Calculating a2 a3 a4 Calculate a2 a2 a1 frac1221 a2 frac12 frac16 frac36 frac16 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

need answers ASAP! Q2-Pg1 (5 points) Solution to recursively defined sequence Given the sequence an defined recursively as - a1=21 - ak=ak1+k(k+1)1 for every integer k>1 You will now use iteration to...

Solution to recursively defined sequence Given the sequence an defined recursively as a1=21 - ak=ak1+k(k+1)1 for every integer k>1 You will now use iteration to guess a solution for this sequence: 1....

Math 221 Discrete Mathematics UOPX Make sure all of the are fresh work with proper citation APA format, no used work will be accepted thanks so much. To be substantive, in addition to meeting the...

BOOK = TEXT SEARCH GOOGLE BOOK 7:14 AM Mon Mar6 on. d2l.oakton.edu 1 . - Tl _ 3. Prove by Induction that 2:31 i(i+1) 4. Prove using induction that 3 | (n3 10n + 9) for all integers n 2 0; that is, n3...

\f\f\f\f\f\f\f\f\f\fSequences, Mathematical Induction and Recursion 1 5.1 Sequences 2 Sequences Sequences represent ordered lists of elements. A sequence is defined as a function from a subset of N...

Describe how to construct the function cpo ((D E), v) of two cpos (D, vD) and (E, vE). Prove that ((D E), v) is a cpo. (You may use facts about least upper bounds provided you state them clearly.)...

Question 1 Our first section of this topic deals with a specific proof technique of mathematical induction. This is an incredibly powerful tool. Fill in the words below to Not yet answered complete...

Suppose B is the set of bit strings recursively defined by: 001 ES Let an the number of bit strings in B of length n, for n 2. Determine a recursive definition for an, ie. determine a2, a3 and a...

What would you imagine to be the major differences among working for a domestic firm inside the United States, working for a foreign companys operations inside the United States, and working for an...

Question (5) (15 Marks) A. What are some of the first indications that a product design or development process. is going badly? B. List FIVE (5) common underlying causes. C. Identify ONE (1)...

answer this Multiple Choice Question Dividends payable is increased on the O date of record. O date of payment. O declaration date. Need help? Review these concept resources

User Defined Functions Write a Python based user defined functions for each of the following questions 1- Indices of Two Numbers Sum Given a list of integers, return indices of the two numbers such...