Question: Now suppose a is any integer relatively prime to p. We take successive powers of a modulo p until we find an instance where a'
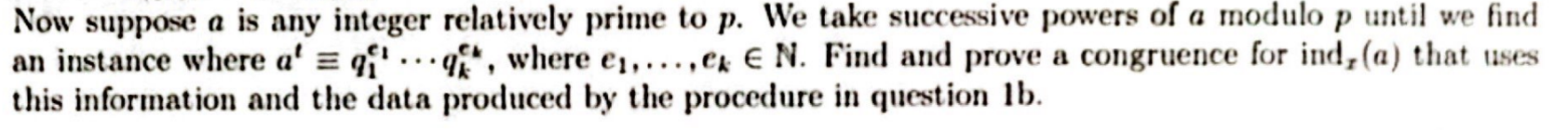

Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


