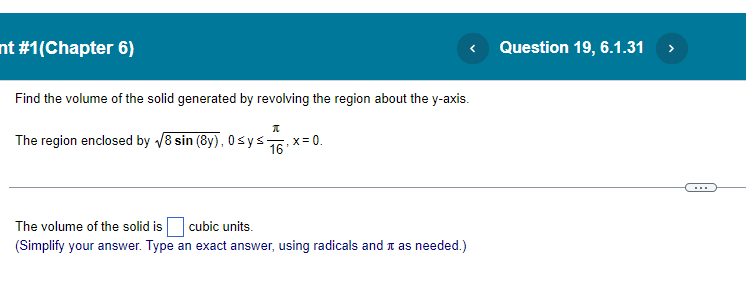
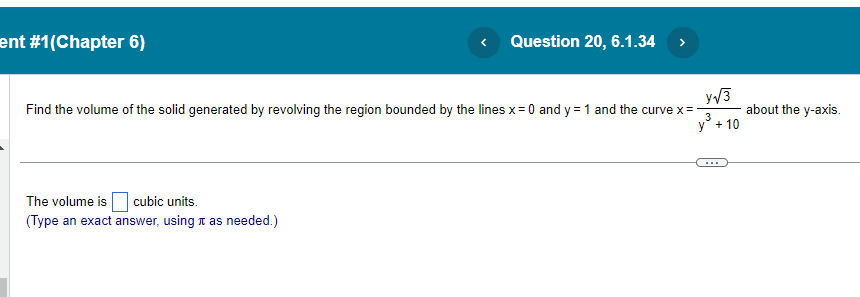
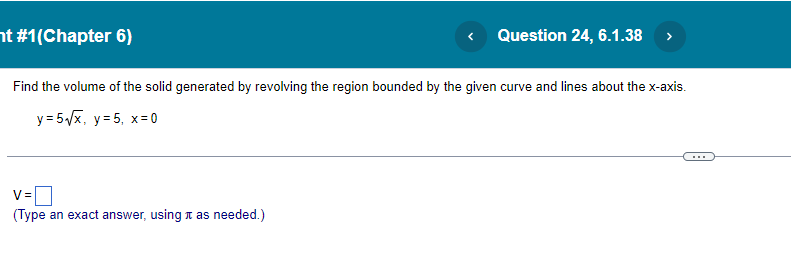
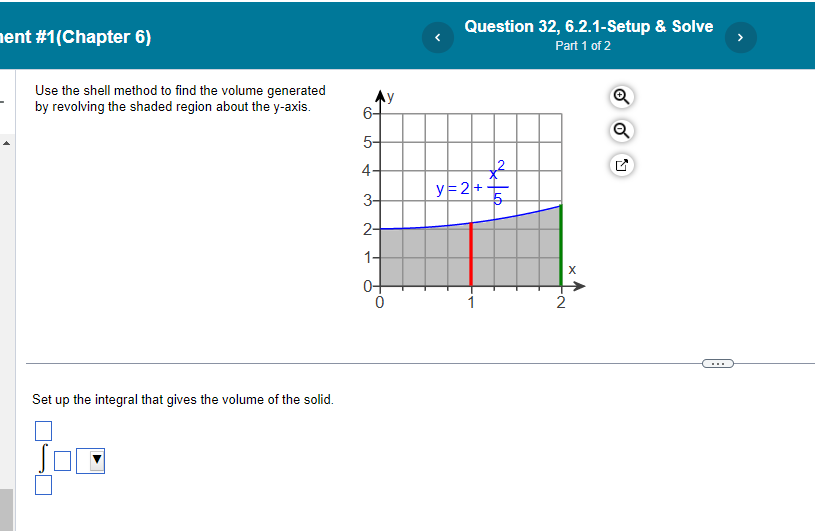
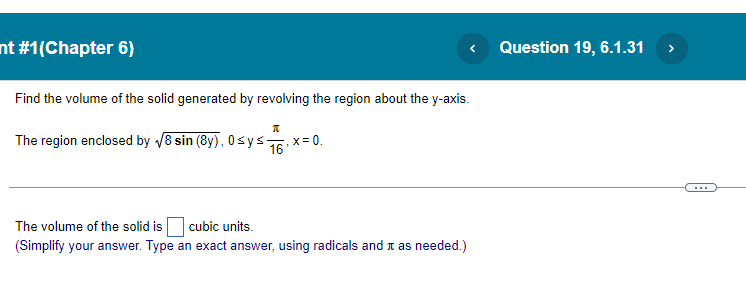
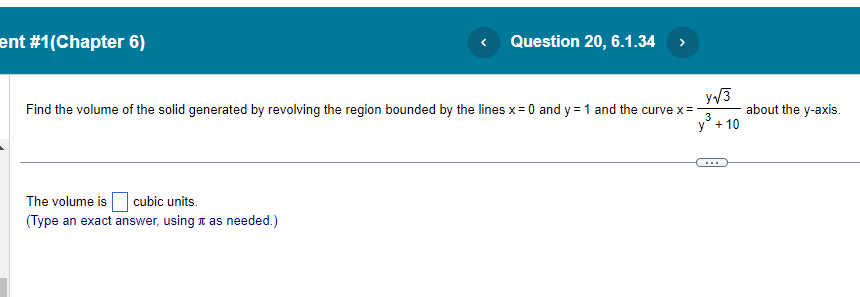
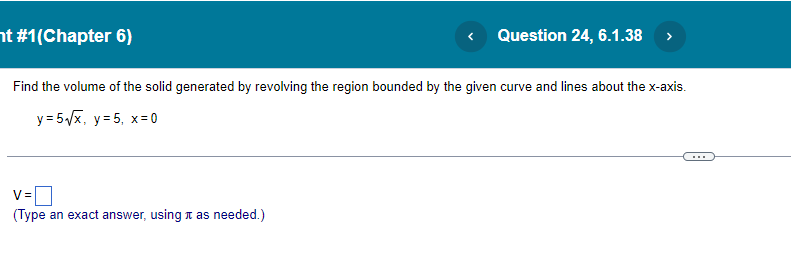
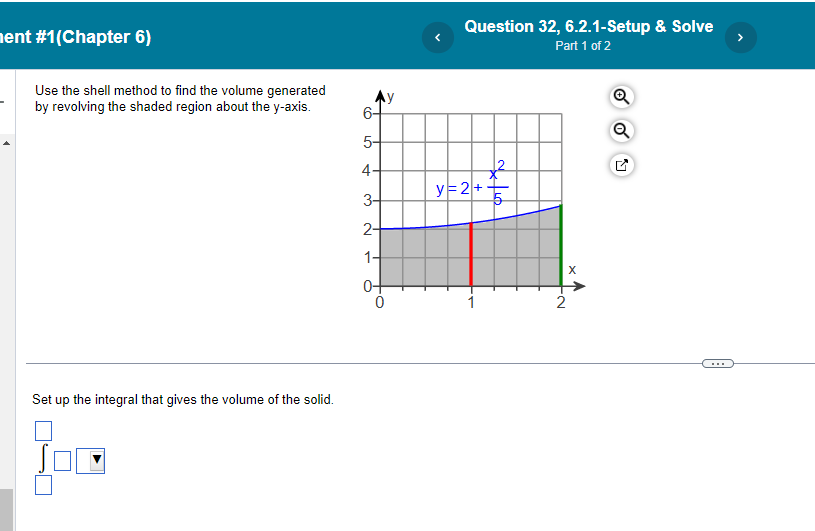
nt #1(Chapter 6) Find the volume of the solid generated by revolving the region about the y-axis. The region enclosed by :8 sin (By) , 0sys- 16 : X=0. The volume of the solid is cubic units. (Simplify your answer. Type an exact answer, using radicals and It as needed.)nt #1[Chapter 6} N3 y3+1| Find the volume of the solid generated by revolving the region bounded by the lines x = [II and v = 1 and the curve x = about the v-axis. <:> The volume is D cubic units. [Type an exact answer: using 11: as needed.) Find the volume of the solid generated by revolving the region bounded by the given curve and lines about the x-exie. 19:54; y=5, x=ti| <: m an exact answer: using as needed. question b.1.4 solve part at: nt find the volume of solid generated by revolving following region about given axis. in rst quadrant bounded above curve y=":3." below xaxis. and on right line x: x="1, (3" use washer method to set up integral that gives solid. v: j we in: shaded y-axis is cubic units. answer it shell y-axis.>