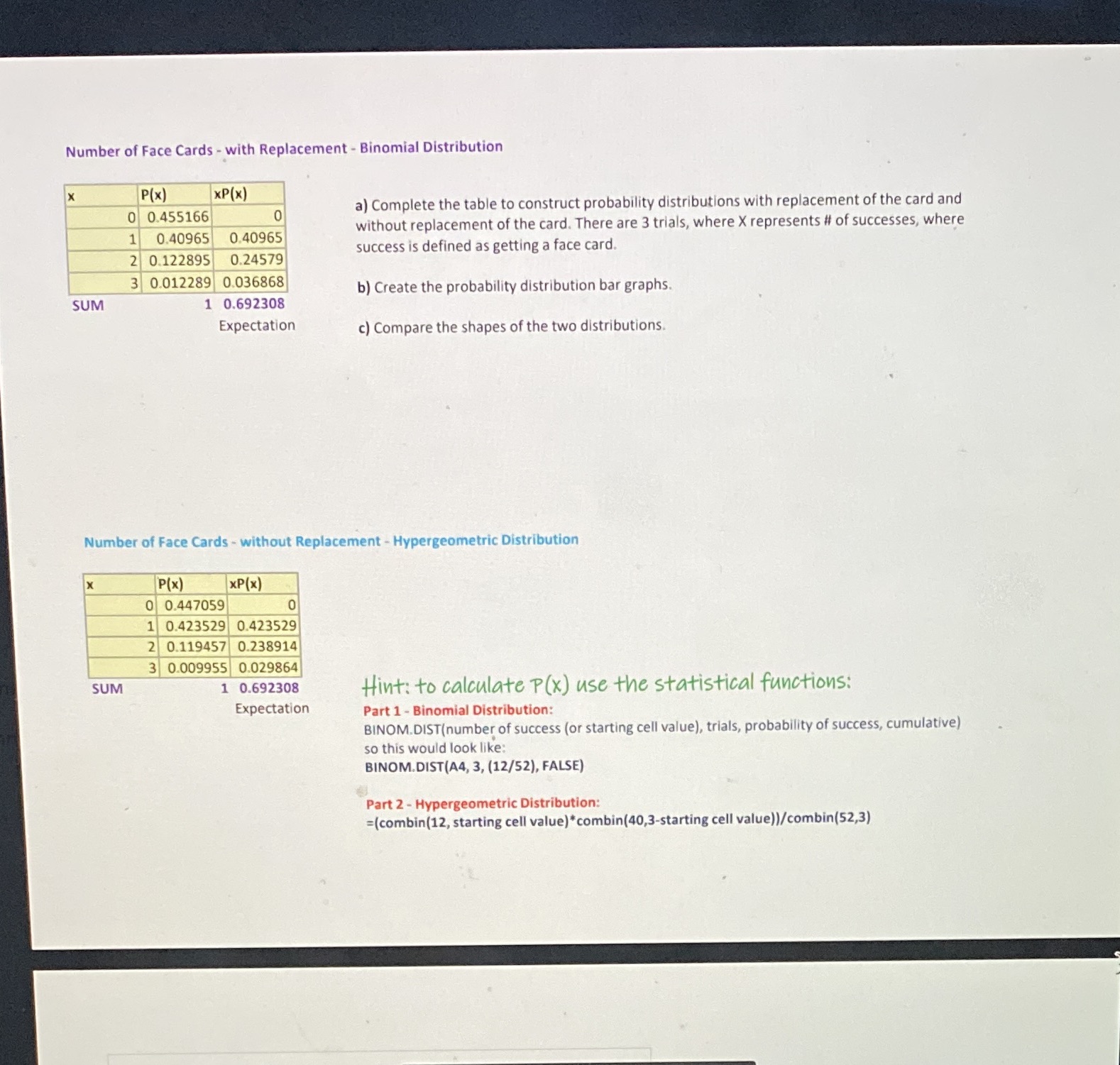
Number of Face Cards - with Replacement - Binomial Distribution P(x) XP(x) 0 0.455166 a) Complete the table to construct probability distributions with replacement of the card and 1 0.40965 0.40965 without replacement of the card. There are 3 trials, where X represents # of successes, where 2 0.122895 0.24579 success is defined as getting a face card. 3 0.012289 0.036868 b) Create the probability distribution bar graphs. SUM 1 0.692308 Expectation c) Compare the shapes of the two distributions. Number of Face Cards - without Replacement - Hypergeometric Distribution P(x) XP(x) 0 0.447059 1 0.423529 0.423529 2 0.119457 0.238914 3 0.009955 0.029864 SUM 1 0.692308 Hint: to calculate P (x) use the statistical functions: Expectation Part 1 - Binomial Distribution: BINOM.DIST(number of success (or starting cell value), trials, probability of success, cumulative) so this would look like: BINOM. DIST(A4, 3, (12/52), FALSE) Part 2 - Hypergeometric Distribution: (combin(12, starting cell value)*combin(40,3-starting cell value))/combin(52,3)