number=float(input('Enter a number (>1): ')) R=int(input('Enter the rooot: ')) error=float(input('Enter the error: '))

x=number/2 cont=0 estimate_error=100

while estimate_error>error: cont=cont+1 if x>number: x_new=x/2 else: x_new=((x+R)/2) x=x_new**R estimate_error=abs((number-x)umber)*100

print(x,estimate_error,cont)

How can I fix this code:

Error:

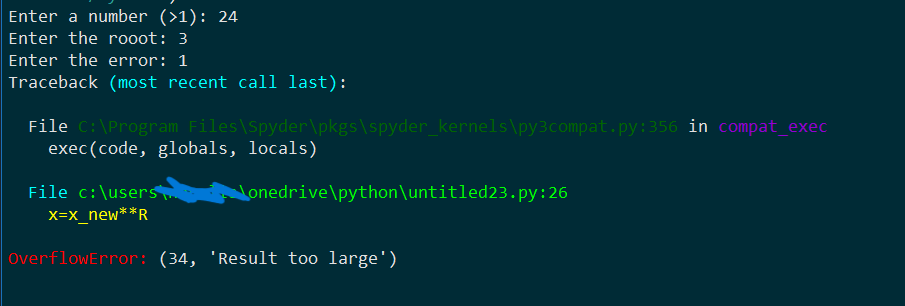
Problem Statement:

Let's say we want to calculate the cube root of 24. We start by assuming that the root we are looking for is equal to the half the number (24/2) and check if that is the root: 12**3=1728 I went over 24, so the number must be smaller than 12 I also know that the number must be greater than zero. My next number to deal with will then be the number which is in the middle between 12 and 0, the 6. We check if 6 is the root I'm looking for: 6**3=216 I went over 24, so the number must be less than 6 and greater than 0. I try then with (0+6)/2=3, I check if 3 is the root that I am looking for: 3**3=27 I went over 24, so the number must be less than 3 and greater than 0. I then try with (0+3)/2=1.5, I check if 1.5 is the root I'm looking for: 1.5**3=3.375 I'm below 24, so the number should be greater than 1.5 and less than 3. I then try (1.5+3)/2=2.25, check if 2.25 is the root I'm looking for: 2.25**3=11.3906 I am below 24, so the number must be greater than 2.25 and less than 3. I then try with (2.25+3)/2=2.625, I check if 2.625 is the root I'm looking for: 2.625**3=18.0879 I'm below 24, so the number must be greater than 2.625 and less than 3. I then try (2.625+3)/2=2.8125, check if 2.8125 is the root I'm looking for: 2.8125**3=22.2473 I'm below 24, so the number must be greater than 2.8125 and less than 3. I try then with (2.8125+3)/2=2.90625, check if 2.90625 is the root I'm looking for: 2.90625**3=24.54703 I went over 24, so the number must be less than 2.90625 and greater than 2.8125. Deal so with (2.8125+2.90625)/2=2.859375, I check if 2.859375 is the root I'm looking for: 2.859375**3=23.37832... and so on forever and ever... Obviously we have to establish a stopping criterion, for example, for each value we can calculate a relative error and decide if we are satisfied with that error. For example, for 2.859375 the error would be abs((24-2.859375**3)/24)*100=2.5903%.

(a) Implement the algorithm explained in the example in a flowchart. The input must be the number to which is to be computed for the root (assuming the user always enters a real number greater than 1), the root to be computed (assume that the user always enters an integer greater than 1, for example 2 for the square root, 3 for the cubic and so on), the error that one is willing to accept. The output should be the estimate of the root, the error associated with that estimate and the number of terms that were used. (b) Same as (a) but implement your algorithm in a Python program. The input/output of your program should be similar to that shown in the figure. Submit a desktop proof and its respective screenshot when it is calculates the fifth root of 123 and the admissible error is 2%.