numbers :

68

20

76

55

561

84

65

20

13

305

128

20

28

196

120

66

60

78

83

30

100

115

160

81

46

98

29

34

40

38

155

45

342

136

6

205

58

65

232

22

67

25

90

409

45

18

145

113

36

100

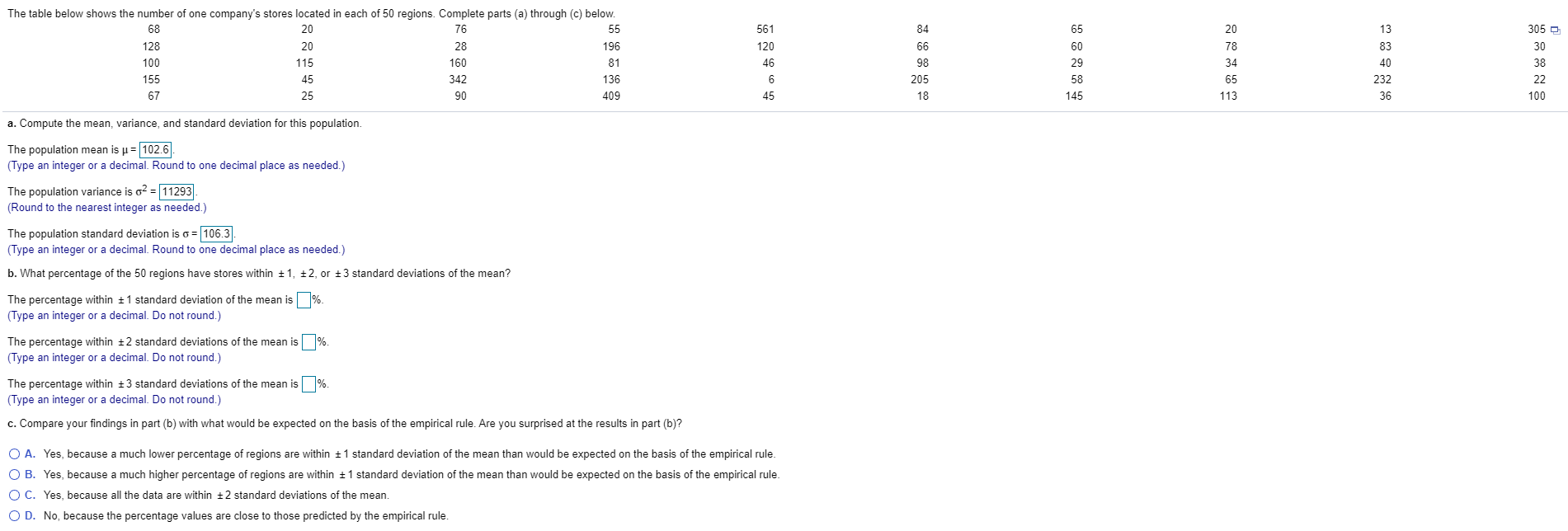
The table below shows the number of one company's stores located in each of 50 regions. Complete parts (a) through (c) below. 68 20 76 55 561 84 65 20 305 0 128 20 28 196 120 66 78 30 100 115 160 81 46 98 29 34 38 155 45 342 136 205 65 232 22 67 25 90 409 45 18 145 113 36 100 a. Compute the mean, variance, and standard deviation for this population. The population mean is u = 102.6 (Type an integer or a decimal. Round to one decimal place as needed.) The population variance is 62 = 11293 (Round to the nearest integer as needed.) The population standard deviation is o = 106.3 (Type an integer or a decimal. Round to one decimal place as needed.) b. What percentage of the 50 regions have stores within + 1, +2, or + 3 standard deviations of the mean? The percentage within 1 1 standard deviation of the mean is% (Type an integer or a decimal. Do not round.) The percentage within 12 standard deviations of the mean is% (Type an integer or a decimal. Do not round. The percentage within 13 standard deviations of the mean is%. (Type an integer or a decimal. Do not round.) c. Compare your findings in part (b) with what would be expected on the basis of the empirical rule. Are you surprised at the results in part (b)? O A. Yes, because a much lower percentage of regions are within 1 1 standard deviation of the mean than would be expected on the basis of the empirical rule. O B. Yes, because a much higher percentage of regions are within 1 1 standard deviation of the mean than would be expected on the basis of the empirical rule. O C. Yes, because all the data are within + 2 standard deviations of the mean O D. No, because the percentage values are close to those predicted by the empirical rule