Numerical analysis I Interpolation and the Lagrange Polynomial questions I have solutions for 9 and 11 but do not understand them.

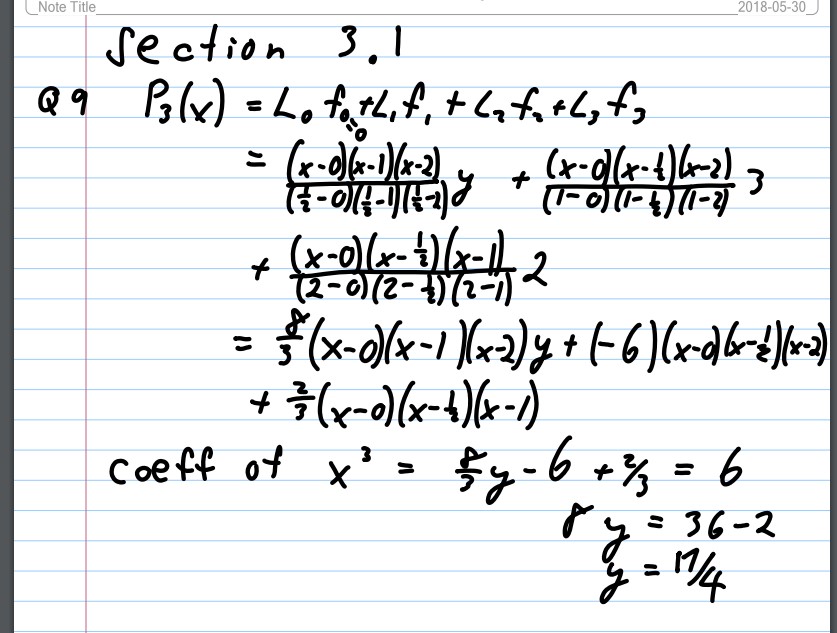
9. Let Py(x) be the interpolating polynomial for the data (0, 0), (0.5, y), (1, 3), and (2, 2). The coefficient of x' in Py(x) is 6. Find y. 10. Let f(x) = vx - x2 and P2(x) be the interpolation polynomial on xo = 0, x, and x2 = 1. Find the largest value of x1 in (0, 1) for which f (0.5) - P2 (0.5) = -0.25. 11. Use the following values and four-digit rounding arithmetic to construct a third Lagrange polyno- mial approximation to f (1.09). The function being approximated is f(x) = log ,(tan x). Use this knowledge to find a bound for the error in the approximation. f(1.00) = 0.1924 /(1.05) = 0.2414 /(1.10) = 0.2933 /(1.15) = 0.349211 P,(X = X-1.65) x - 1.10 x- 1.15) (1.00 -1.05) ( 1.00 -1. 10) (1.60 -1.15) X . 1924 + (x - 1.00) ( x - 1.10) ( x-1.15) (1.65-1.00) (1.65 -1.10) ( 1.05 -1.15) * . 2414 + (x - 1.00) ( x - 1.05) (x - 1. 15) (1. 10- 1.00) (1.10- 1.05 ) ( 1.10-1.15) x . 2 933 + x - 1.00) (x -1.05) (x -1. 10) , x 39 92 1. 15 -1. 00) (1.15-1.05) (1.15- 1.10) P ( 1.09) = 0.2826 . abos error: lag,. (ton (1.09)) - P(1.09)= 4.3 x10-5 Error bound is a bit, messy! The 4 th derivative is ( by Wolfram Alpha) log 10 This is an increases function which equals 81.5683 at the endot 6.15.Thus the error bound is 81. 5083 (1.09-1)(1.09-1.05)(1.09-1.1)( 1.09-1.15)1 2 7.4 x 10 - 6 The discrepancy tv due to the fact that othe ata are Given to only four decimal placen of Jonly toun - dig it athmeh'c Oused.\f