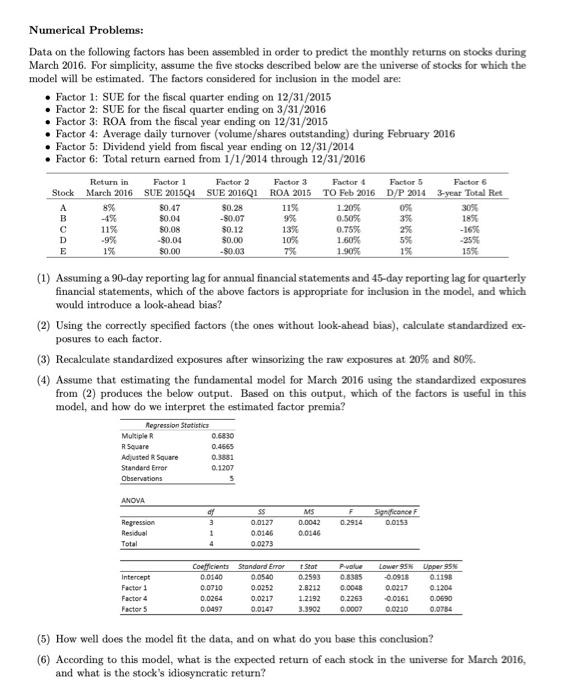
Numerical Problems: Data on the following factors has been assembled in order to predict the monthly returns on stocks during March 2016. For simplicity, assume the five stocks described below are the universe of stocks for which the model will be estimated. The factors considered for inclusion in the model are: Factor 1: SUE for the fiscal quarter ending on 12/31/2015 Factor 2: SUE for the fiscal quarter ending on 3/31/2016 Factor 3: ROA from the fiscal year ending on 12/31/2015 Factor 4: Average daily turnover (volume/shares outstanding) during February 2016 Factor 5: Dividend yield from fiscal year ending on 12/31/2014 Factor 6: Total return carned from 1/1/2014 through 12/31/2016 Stock A B D E Return in Factor 1 Factor 2 Factor 3 Factor Factor 5 Factor 6 March 2016 SUE 2015Q4 SUE 2016Q1 ROA 2015 TO Feb 2016 D/P 2014 3-year Total Ret 8% 80.47 $0.28 11% 1.20% 0% 30% -4% $0.04 -$0.07 9% 0.50% 3% 185 11% 50.08 $0.12 13% 0.75% -16% -9% -$0.04 $0.00 10% 1.60% 5% -255 1% $0.00 7% 1.90% 1% 15% (1) Assuming a 90-day reporting lag for annual financial statements and 45-day reporting lag for quarterly financial statements, which of the above factors is appropriate for inclusion in the model, and which would introduce a look-ahead bias? (2) Using the correctly specified factors (the ones without look-ahead bias), calculate standardized ex- posures to each factor (3) Recalculate standardized exposures after winsorizing the raw exposures at 20% and 80%. (4) Assume that estimating the fundamental model for March 2016 using the standardized exposures from (2) produces the below output. Based on this output, which of the factors is useful in this model, and how do we interpret the estimated factor premia? Repression Statistics Multiple R R Souare Adjusted R Square Standard Error Observations 0.6830 0.4565 0.3831 0.1207 5 ANOVA F 0.2914 Significance 0.0153 Regression Residual Total of 3 1 4 MS 0.0042 0.0146 SS 0.0127 0.0146 0.0273 Intercept Factor 1 Factor 4 Factor 5 Coefficients Standard Error 0.0140 0.05.40 0.0710 0.0252 0.0254 0.0217 0.0497 0.0147 Star 0.2593 2.8212 1.2192 3.3902 P-value 0.8385 0.0048 0.2263 0.0007 Lower 95 Upper 95% 0.0955 0.1198 0.0217 0.1204 -0.0163 0.0690 0.0230 0.0784 (5) How well does the model fit the data, and on what do you base this conclusion? (6) According to this model, what is the expected return of each stock in the universe for March 2016, and what is the stock's idiosyncratic return? Numerical Problems: Data on the following factors has been assembled in order to predict the monthly returns on stocks during March 2016. For simplicity, assume the five stocks described below are the universe of stocks for which the model will be estimated. The factors considered for inclusion in the model are: Factor 1: SUE for the fiscal quarter ending on 12/31/2015 Factor 2: SUE for the fiscal quarter ending on 3/31/2016 Factor 3: ROA from the fiscal year ending on 12/31/2015 Factor 4: Average daily turnover (volume/shares outstanding) during February 2016 Factor 5: Dividend yield from fiscal year ending on 12/31/2014 Factor 6: Total return carned from 1/1/2014 through 12/31/2016 Stock A B D E Return in Factor 1 Factor 2 Factor 3 Factor Factor 5 Factor 6 March 2016 SUE 2015Q4 SUE 2016Q1 ROA 2015 TO Feb 2016 D/P 2014 3-year Total Ret 8% 80.47 $0.28 11% 1.20% 0% 30% -4% $0.04 -$0.07 9% 0.50% 3% 185 11% 50.08 $0.12 13% 0.75% -16% -9% -$0.04 $0.00 10% 1.60% 5% -255 1% $0.00 7% 1.90% 1% 15% (1) Assuming a 90-day reporting lag for annual financial statements and 45-day reporting lag for quarterly financial statements, which of the above factors is appropriate for inclusion in the model, and which would introduce a look-ahead bias? (2) Using the correctly specified factors (the ones without look-ahead bias), calculate standardized ex- posures to each factor (3) Recalculate standardized exposures after winsorizing the raw exposures at 20% and 80%. (4) Assume that estimating the fundamental model for March 2016 using the standardized exposures from (2) produces the below output. Based on this output, which of the factors is useful in this model, and how do we interpret the estimated factor premia? Repression Statistics Multiple R R Souare Adjusted R Square Standard Error Observations 0.6830 0.4565 0.3831 0.1207 5 ANOVA F 0.2914 Significance 0.0153 Regression Residual Total of 3 1 4 MS 0.0042 0.0146 SS 0.0127 0.0146 0.0273 Intercept Factor 1 Factor 4 Factor 5 Coefficients Standard Error 0.0140 0.05.40 0.0710 0.0252 0.0254 0.0217 0.0497 0.0147 Star 0.2593 2.8212 1.2192 3.3902 P-value 0.8385 0.0048 0.2263 0.0007 Lower 95 Upper 95% 0.0955 0.1198 0.0217 0.1204 -0.0163 0.0690 0.0230 0.0784 (5) How well does the model fit the data, and on what do you base this conclusion? (6) According to this model, what is the expected return of each stock in the universe for March 2016, and what is the stock's idiosyncratic return