Objective Function:

Minimize the total cost: Cost $=4$x $+12$y

Constraints:

$1.$Orange requirement: $0\mathrm{.}06$x $+0\mathrm{.}04$y $5$

$2.$Mango requirement: $0\mathrm{.}04$x $+0\mathrm{.}08$y $5$

$3.$Lime limit: $0\mathrm{.}02$x $+0\mathrm{.}07$y $6$

$4.$Total amount: x $+$ y $100$

Non$-$negativity: x $0,$ y $0$

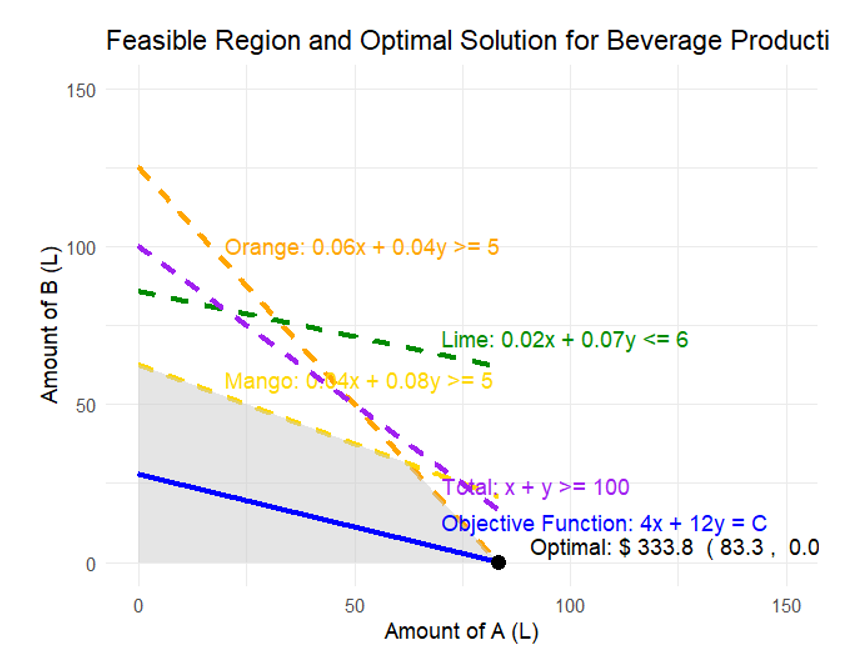
Based on the above graph, we can infer the below points.

$$The feasible region is the shaded gray area

$$The optimal solution is at $(83\mathrm{.}3$ L$,0$ L$)$ for Products A and B

$$The minimal cost for the optimal solution is $$333\mathrm{.}8$

Based on above datapoints, Is there a range for the cost $($$$)$ of A that can be changed without affecting the optimum solution obtained above? If so$,$ what is the range?