Objectives: The projects in this course are designed to allow you to use the tools of calculus you have learned so far to analyze a data set and draw conclusions. The projects are a chance for you to:

• Apply your mathematical tools in a real-world context.
• Learn to work on a team, building off each other's strengths.
• Become proficient with using software to analyze and manipulate data.
• Develop skills and communicating your results in context.
• Analyze the behavior of the rate of change of the logistic function.
• Derive and solve the differential equation for the logistic function.

Data Source: Samanlioglu, Funda, and Ayse Humeyra Bilge. "An Overview of the 2009 A(H1N1) Pandemic in Europe: Efficiency of the Vaccination and Healthcare Strategies." Journal of healthcare engineering vol. 2016 (2016): 5965836. doi:10.1155/2016/5965836 (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5058565/)

Directions:. Include any graphs or other tables appropriately formatted and labeled

STEPS/ Assignment: REVIEW real data from the H1N1 2009 flu pandemic showing the cumulative deaths in Europe, weeks 36-68 of the outbreak. The origin of the word epidemic is Greek, where epi means "upon" and demic means "the people". When the disease affects several geographic regions at the same, it is called a pandemic (from Greek pan meaning "all".) Epidemiology is the scientific study of contagious diseases, and it deals with the essential features of the disease, in particular, the math behind modeling the rate of infection.In this assignment, we will model and study the infection rates for the H1N1.

1. SEE Table 1 BELOW. This data tracks the cumulative number of deaths in Europe from the H1N1 virus during weeks 36-68. Plot any three different trendline options in excel to plot against this data (except moving average). For this data, briefly describe why the three choices you chose are not good fits to the data based on the behavior of the function. Include the three plots in your report
2. Briefly describe the logistic regression and why it would be a good fit for this data. Notice (sadly) that excel does not have a logistic regression option. Let's use calculus to help find this regression curve.
3. On Table 1 in Excel, let N(t) be the function that gives the cumulative number of deaths in week t. Add a new column to Table 1 where you approximate the "death rate" of the disease (the rate of change) using dN/dt = delta N / delta t .Round your values to one decimal place. Leave the first cell blank as there is no prior data to find delta N / delta t .
4. In Excel, a new two column table (call it Table 2) to analyze the rate of change dN/dt as a function of time.
   1. Label the first column, "NewWeek", and the second column "Death Rate".
   2. Start "NewWeek" at 0 and populate the column by subtracting 36 from each Week value.
   3. Use the death rate values to populate this second column from the prior step. (Week 0 will not have a death rate.)
   4. Once the table is complete, a scatterplot of the data. Label your axes and title the graph.
5. Explain the properties of the rate of change of N(t) based on this scatterplot. Relate it to the spread of a disease. Include the scatterplot in your report.
6. a new two column table in Excel (call it Table 3).
   1. The first column header will be "N(t)*(A-N(t))", where A horizontal asymptote of the data.Use A = 1261 for this data as that is the last data value on the table.
   2. Populate the first column of the data using a formula in Excel to find N(t)*(A-N(t))",
   3. Populate the second column with the growth rate dN/dt data from Table 2.
   4. Create a scatterplot of this table. Label your axes and title the graph.
7. What does the value A-N(t) represent?
8. a linear regression in Excel describe the mathematical relationship between the variables on the Scatterplot from Table 3. On the scatterplot, show the regression, its equation, and analyze the residual R. Set the intercept of the linear regression to zero (by checking the box near 'display equation'.) Include this graph
9. Based on your findings in the previous step, derive a differential equation of the form dN/dt = ... (Hint: think about what y and x are representing in the previous problem.)
10. Solve this differential equation to find the Logistic Regression with the initial condition N(0) = 7from the data. Show all the steps of your solution.
11. Since Excel is not great at plotting continuous functions, open desmos.com. Copy and paste the original Table 1 values from Excel into Desmos. This will create a table in Desmos and a scatterplot.
12. In Desmos, graph the solution you found to the differential equation. See how well your logistic equation fits the data. Because the initial condition used was N(0) = 7 shifted the date by 36. your graph will be shifted left by 36 units. Fix this by horizontally shifting your function right by 36 to match the data. (Hint: what substitution do you make for x to do this?)
13. Checkpoint: If your logistic regression fits the data pretty well, congratulations! You have done what excel cannot. Include a picture of your curve fit to the data in your report.
14. Unlike Excel, Desmos can do Logistic Regressions. In Desmos, below the table of data, enter the following formula using "x₁" and "y₁", which will model the data using a logistic regression:

For extra help creating regressions, see https://learn.desmos.com/regressions. Include a picture of the graph with both functions (yours and Desmos') fit to the data in your report.

1. Describe Desmos's regression function qualitatively.Is it a good fit of the data? Describe and interpret its behavior at infinity.
2. Explain what the sign of the first derivative N'(t) tells us about the model.
3. Explain what the sign of the second derivative N''(t) tells us about the model.
4. Find the week where the death rate starts to slow down

1. Describe the domain and range of the two functions.Explain the differences between the coefficients A and B in the logistic function you found by solving the differential equation and the one found by Desmos.
2. Which curve best models the data: the one found by solving the differential equation or the logistic regression found using desmos? Why is one better than the other? Give a reason other than "it goes through more data points."

TABLE 1 - build new tables from this, I think not sure

Week	Cum. Deaths
36	7
37	12
38	13
39	12
40	14
41	14
42	21
43	29
44	70.9
45	113.3
46	156
47	167
48	306
49	410
50	548
51	598
52	702
53	806
54	917
55	1004
56	1072
57	1123
58	1158
59	1187
60	1210
61	1227
62	1233
63	1238
64	1247
65	1253
66	1258
67	1259
68	1261

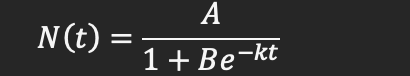\f