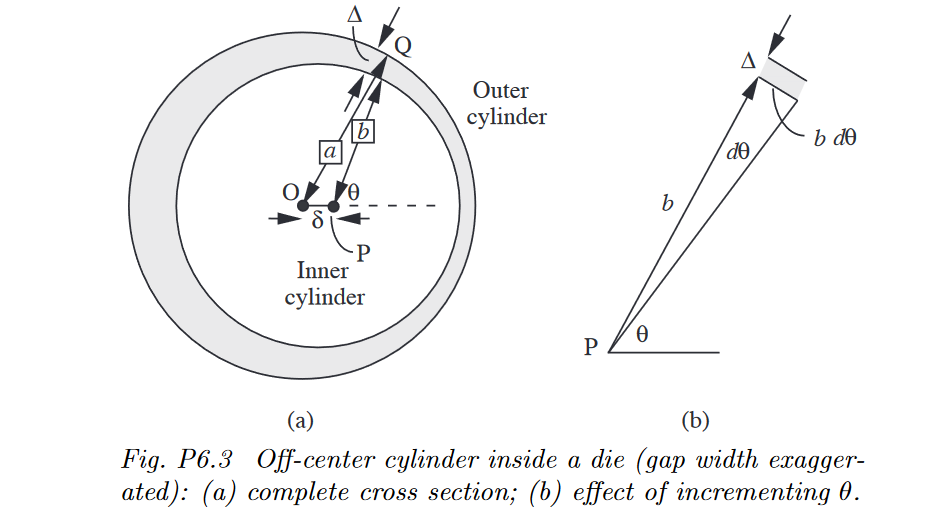
Off$-$center annular flow$$D $($C$).$ A liquid flows under a pressure gradient $$p$/$z through the narrow annular space of a die, a cross section of which is shown in Fig. P$6\mathrm{.}3($a$).$ The coordinate z is in the axial direction, normal to the plane of the diagram. The die consists of a solid inner cylinder with center P and radius b inside a hollow outer cylinder with center O and radius a$.$ The points O and P were intended to coincide but, due to an imperfection of assembly, are separated by a small distance $.$

By a simple geometrical argument based on the triangle OPQ, show that the gap width $$ between the two cylinders is given approximately by: $.=$ a $$ b $$ cos $,$ where the angle is defined in the diagram. Now consider the radius arm b swung through an angle d$,$ so that it traces an arc of length bd$.$ The flow rate dQ through the shaded element in $($b$)$ is approximately that between parallel plates of width bd and separation $.$ Hence, prove that the flow rate through the die is given approximately by: Q $=$ bc$(2$$3+3$$2),$ in which: c $=112$ $$p $$z $,$ and $=$ a $$ b$.$ Assume from Eqn. $($E$6\mathrm{.}1\mathrm{.}26)$ that the flow rate per unit width between two flat plates separated by a distance h is: h$312$ $$p $$z $.$ What is the ratio of the flow rate if the two cylinders are touching at one point to the flow rate if they are concentric? $($a$)$

$($b$)$

Fig. P$6\mathrm{.}3$ Off$-$center cylinder inside a die $($gap width exaggerated$)$: $($a$)$ complete cross section; $($b$)$ effect of incrementing $\backslash (\backslash$theta $\backslash ).$