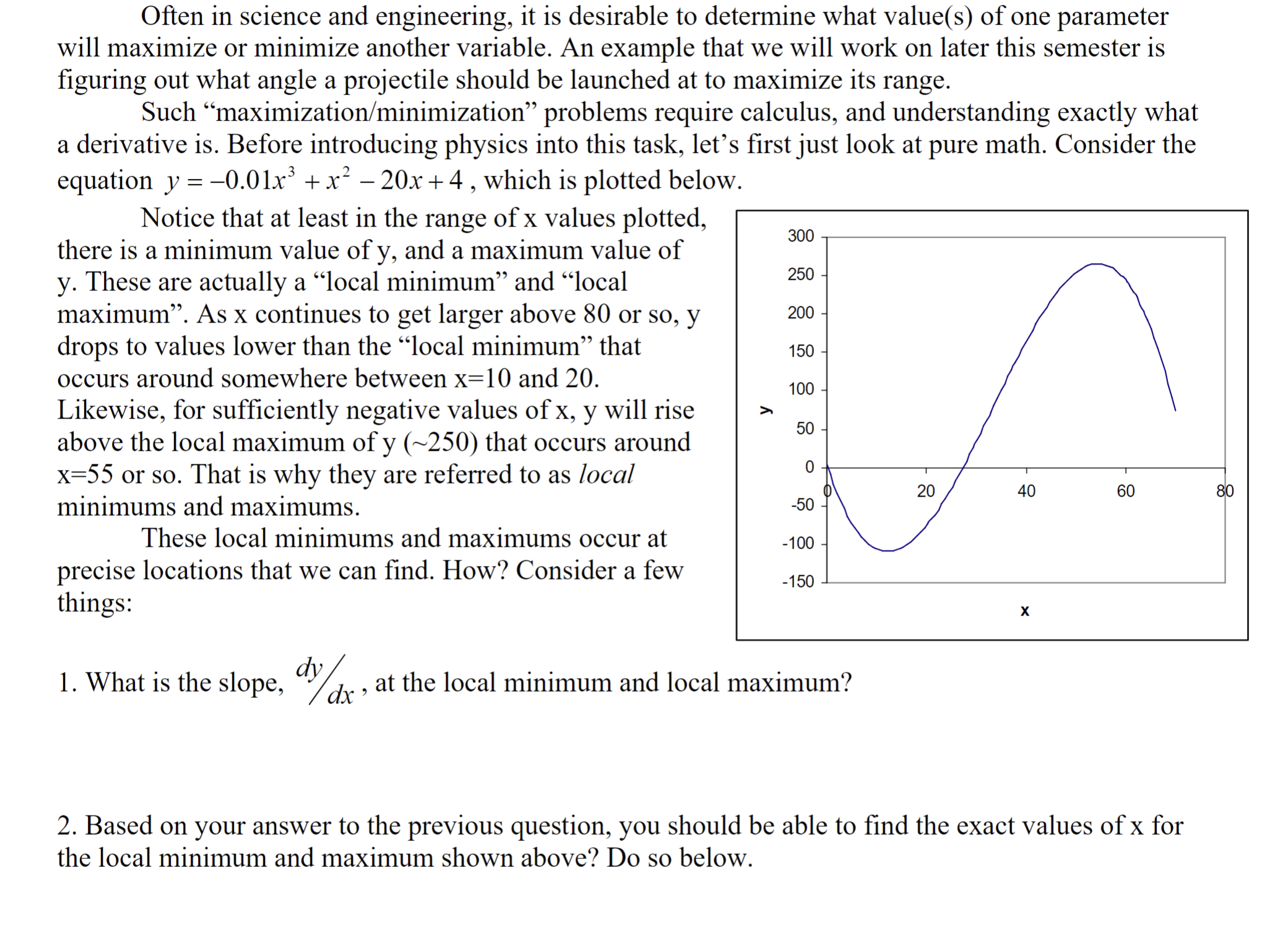
Often in science and engineering, it is desirable to determine what value(s) of one parameter will maximize or minimize another variable. An example that we will work on later this semester is figuring out what angle a projectile should be launched at to maximize its range. Such "maximization/minimization" problems require calculus, and understanding exactly what a derivative is. Before introducing physics into this task, let's first just look at pure math. Consider the equation y = 0.01x + x - 20x+4, which is plotted below. Notice that at least in the range of x values plotted, there is a minimum value of y, and a maximum value of y. These are actually a "local minimum" and "local maximum". As x continues to get larger above 80 or so, y drops to values lower than the local minimum that occurs around somewhere between x=10 and 20. Likewise, for sufficiently negative values of x, y will rise above the local maximum of y (~250) that occurs around x=55 or so. That is why they are referred to as local minimums and maximums. These local minimums and maximums occur at precise locations that we can find. How? Consider a few things: 300 250 200 150 100 50 50 0 20 -50 -100 -150 1. What is the slope, dy/dx, at the local minimum and local maximum? 20 40 40 X 60 60 2. Based on your answer to the previous question, you should be able to find the exact values of x for the local minimum and maximum shown above? Do so below. 80 0