Old MathJax webview

remember i only want C

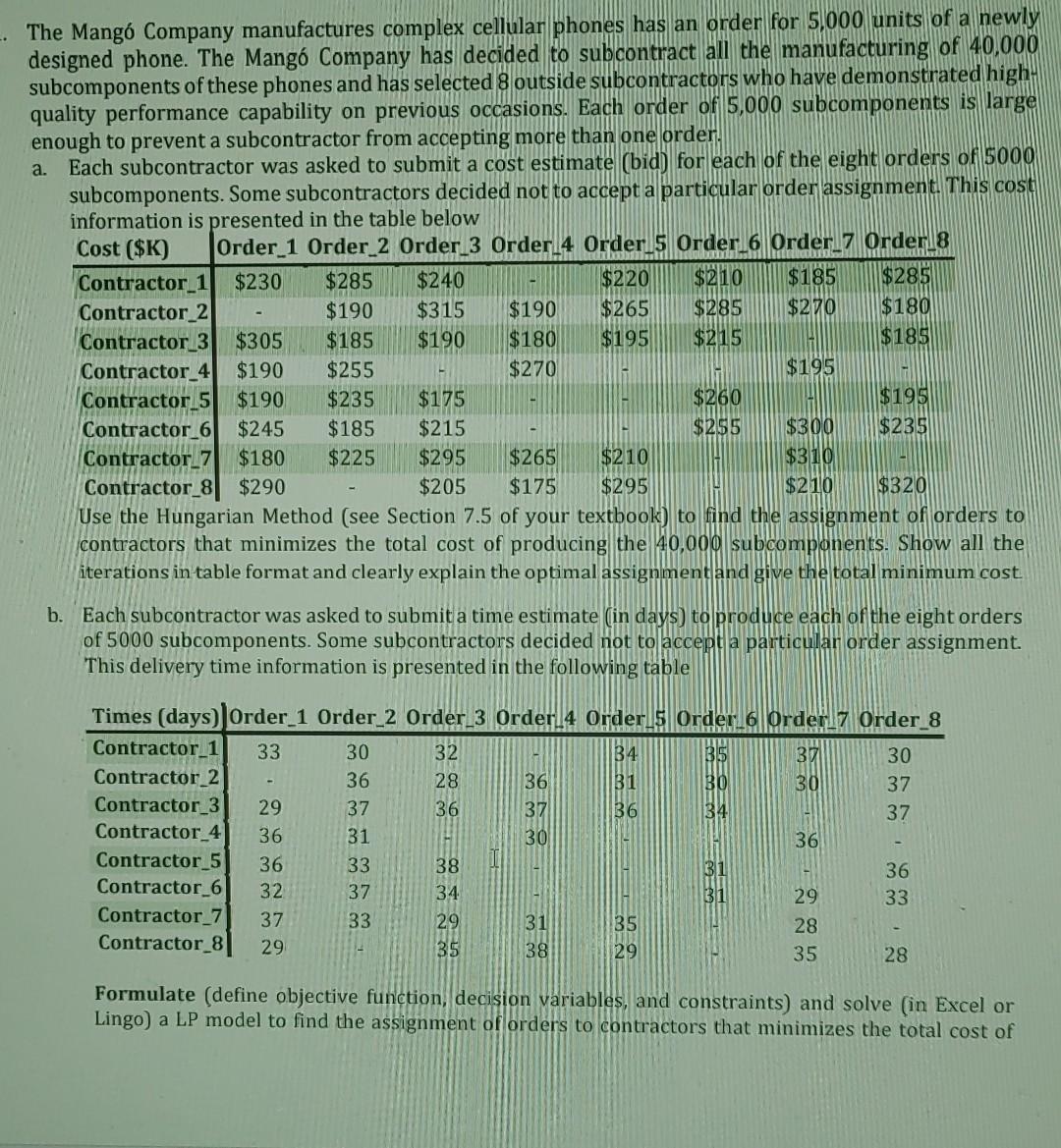
C. Using the information given in (a) and (b), Formulate (define objective function, decision variables, and constraints) and solve (in Excel or Lingo) a LP model to find the assignment of orders to contractors that minimizes the total cost of producing the 40,000 subcomponents and, at the same time, production of phones can be started in 34 days or less. 2. Suppose there is - The Mang Company manufactures complex cellular phones has an order for 5,000 units of a newly designed phone. The Mang Company has decided to subcontract all the manufacturing of 40,000 subcomponents of these phones and has selected 8 outside subcontractors who have demonstrated high- quality performance capability on previous occasions. Each order of 5,000 subcomponents is large enough to prevent a subcontractor from accepting more than one order. a. Each subcontractor was asked to submit a cost estimate (bid) for each of the eight orders of 5000 subcomponents. Some subcontractors decided not to accept a particular order assignment. This cost information is presented in the table below Cost ($K) Order 1 Order 2 Order 3 Order 4 Order 5 Order 6 Order 7 Order 8 Contractor_1 $230 $285 $240 $220 $210 $185 $285 Contractor 2 $190 $315 $190 $265 $285 $270 $180 Contractor 3 $305 $185 $190 $180 $195 $215 $185 Contractor_4 $190 $255 $270 $195 Contractor 5 $190 $175 $260 $195 Contractor 6 $245 $185 $215 $255 $300 $235 Contractor 7 $180 $225 $295 $265 $210 $310 Contractor 8 $290 $205 $175 $295 $210 $320 Use the Hungarian Method (see Section 7.5 of your textbook) to find the assignment of orders to contractors that minimizes the total cost of producing the 40,000 subcomponents. Show all the iterations in table format and clearly explain the optimal assignment and give the total minimum cost $235 b. Each subcontractor was asked to submit a time estimate (in days) to produce each of the eight orders of 5000 subcomponents. Some subcontractors decided not to accept a particular order assignment. This delivery time information is presented in the following table Times (days) Order_1 Order_2 Order_3 Order 4 Order 5 Order 6 Order 7 Order_8 Contractor 1 33 30 32 34 35 37 30 Contractor 2 36 28 36 31 BO 30 37 Contractor_3 29 37 36 37 36 34 37 Contractor 4 36 31 30 36 Contractor 5 36 33 38 31 36 Contractor_6 32 37 34 29 33 Contractor 7 37 33 29 31 35 28 Contractor_8 29 35 38 29 35 28 Formulate (define objective function, decision variables, and constraints) and solve in Excel or Lingo) a LP model to find the assignment of orders to contractors that minimizes the total cost of producing the 40,000 subcomponents and that can be started as early as possible. The completion time, CT, is the time when all orders have been produced and delivered. For example, if one assigns Order 1 to Contractor 7 (37 days), Order 2 to Contractor 6 (37 days), Order 3 to Contractor 5 (38 days), Order 4 to Contractor 8 (38 days), Order 5 to Contractor 3 (36 days), Order 6 to Contractor 1 (35 days), Order 7 to Contractor 4 (36 days), and Order 8 to Contractor 2 (37 days), all orders would have been completed by CT = 38 days (the maximum of all delivery times). C. Using the information given in (a) and (b), Formulate (define objective function, decision variables, and constraints) and solve (in Excel or Lingo) a LP model to find the assignment of orders to contractors that minimizes the total cost of producing the 40,000 subcomponents and, at the same time, production of phones can be started in 34 days or less