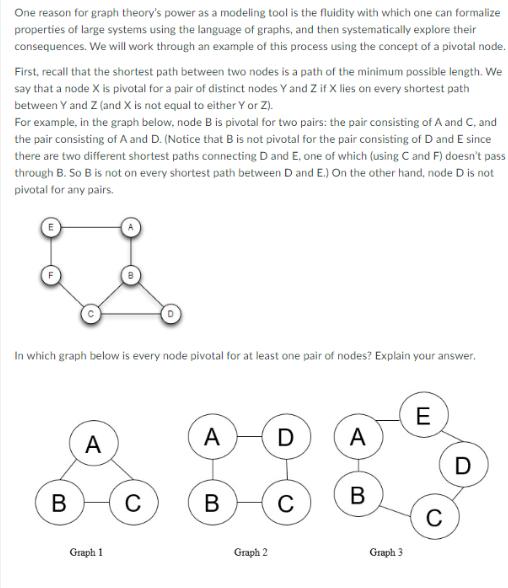
One reason for graph theory's power as a modeling tool is the fluidity with which one can formalize properties of large systems using the language of graphs, and then systematically explore their consequences. We will work through an example of this process using the concept of a pivotal node. First, recall that the shortest path between two nodes is a path of the minimum possible length. We say that a node X is pivotal for a pair of distinct nodes Y and Z if X lies on every shortest path between Y and Z (and X is not equal to either y or Z). For example, in the graph below, node B is pivotal for two pairs: the pair consisting of A and C, and the pair consisting of A and D. (Notice that B is not pivotal for the pair consisting of D and E since there are two different shortest paths connecting D and E, one of which (using C and F) doesn't pass through B. So B is not on every shortest path between D and E.) On the other hand, node D is not pivotal for any pairs. In which graph below is every node pivotal for at least one pair of nodes? Explain your answer. B A Graph 1 C A B Graph 2 D C A B Graph 3 E C D