Question: only answer the last red box (1 point) A stock will pay a dividend D att = tp to the stock price no longer includes
only answer the last red box


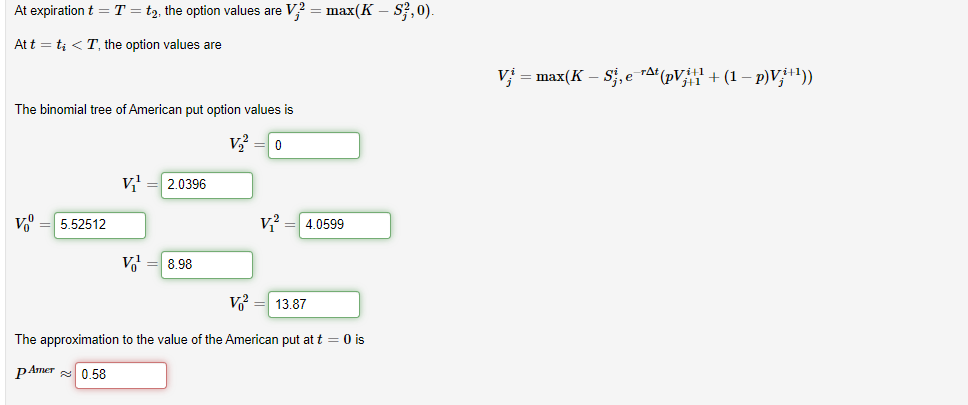
(1 point) A stock will pay a dividend D att = tp
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


