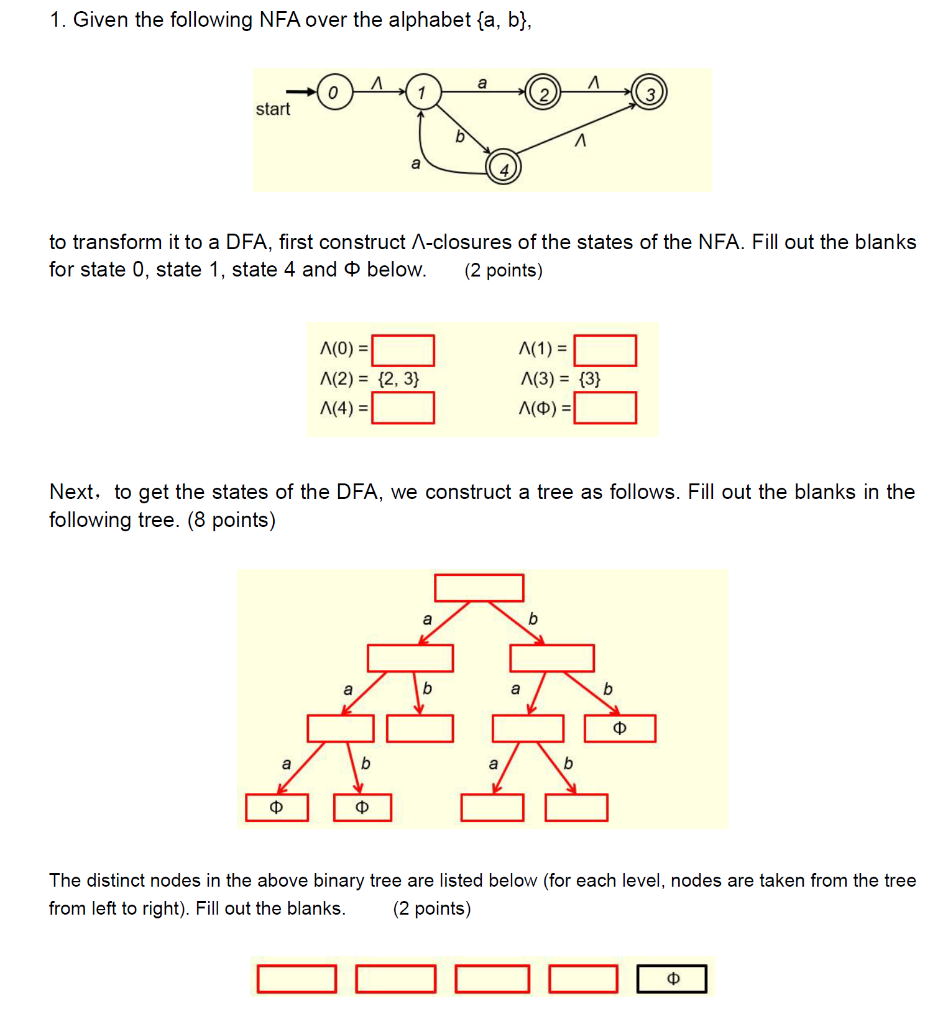
ONLY DO #3ONLY DO #3

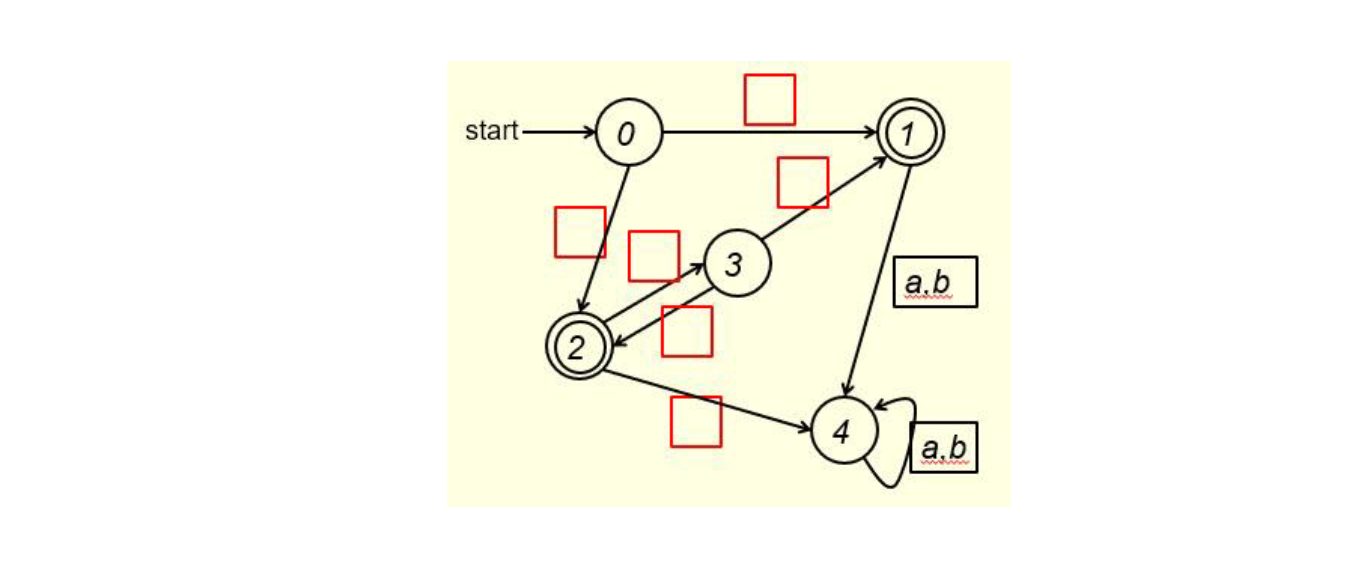
1. Given the following NFA over the alphabet {a, b}, ster-040 40 to transform it to a DFA, first construct A-closures of the states of the NFA. Fill out the blanks for state 0, state 1, state 4 and 0 below. (2 points) A(1) = A(0) = A(2) = {2,3} A(4) = 112) = 12,3) 103) = 413 A(0) = Next, to get the states of the DFA, we construct a tree as follows. Fill out the blanks in the following tree. (8 points) The distinct nodes in the above binary tree are listed below (for each level, nodes are taken from the tree from left to right). Fill out the blanks. (2 points) 2. The above states are the states of the DFA to be constructed for the NFA given in Question #1. We have the following transition table for this DFA. Fill out the blanks in the table. (5 points) | TIT Now replace the five states from top down with 0, 1, 2, 3 and 4, respectively, the transition table of the DFA is of the following form. Fill out the blanks in the table. (3 points) | To 0 s 4 4 2 3 Hence, a DFA can be constructed as follows. Fill out the blanks in the DFA (3 points) start 3. Expression of the NFA given in Question #1 is (2 points) Expression of the DFA you constructed in Question #2 is (2 points) These two expressions are equal, i.e., languages of these two expressions are the same. 1. Given the following NFA over the alphabet {a, b}, ster-040 40 to transform it to a DFA, first construct A-closures of the states of the NFA. Fill out the blanks for state 0, state 1, state 4 and 0 below. (2 points) A(1) = A(0) = A(2) = {2,3} A(4) = 112) = 12,3) 103) = 413 A(0) = Next, to get the states of the DFA, we construct a tree as follows. Fill out the blanks in the following tree. (8 points) The distinct nodes in the above binary tree are listed below (for each level, nodes are taken from the tree from left to right). Fill out the blanks. (2 points) 2. The above states are the states of the DFA to be constructed for the NFA given in Question #1. We have the following transition table for this DFA. Fill out the blanks in the table. (5 points) | TIT Now replace the five states from top down with 0, 1, 2, 3 and 4, respectively, the transition table of the DFA is of the following form. Fill out the blanks in the table. (3 points) | To 0 s 4 4 2 3 Hence, a DFA can be constructed as follows. Fill out the blanks in the DFA (3 points) start 3. Expression of the NFA given in Question #1 is (2 points) Expression of the DFA you constructed in Question #2 is (2 points) These two expressions are equal, i.e., languages of these two expressions are the same