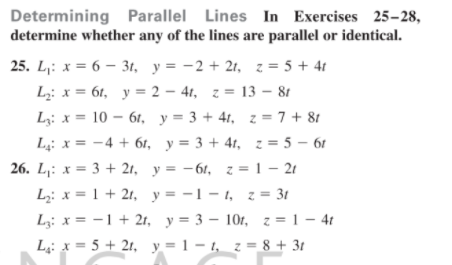ONLY DO 6, 10, 16,26,30

Finding Parametric and Symmetric Equations In Exercises 3-8, find sets of (a) parametric equations and (b) symmetric equations of the line through the point parallel to the given vector or line (if possible). (For each line, write the direction numbers as integers.) Point Parallel to 3. (0, 0, 0) V = (3, 1, 5) 4. (0, 0, 0) v = ( -2, 3, 1) 5. (-2, 0, 3) v = 2i + 4j - 2k 6. (-3, 0, 2) v = 6j + 3k 7. (1, 0, 1) x = 3 + 34,y = 5 - 21.2= -7+1 y +1 8. (-3, 5. 4) =2-3 3 -2Finding Parametric and Symmetric Equations In Exercises 9-12, find sets of (a) parametric equations and (b) symmetric equations of the line through the two points (if possible). (For each line, write the direction numbers as integers.) 9. (5, -3, -2). (-3.3. 1) 10. (0, 4, 3), (- 1, 2, 5) 11. (7, -2, 6). (-3, 0, 6) 12. (0, 0, 25), (10, 10, 0)Finding Parametric Equations In Exercises 13-20, find a set of parametric equations of the line. 13. The line passes through the point (2, 3, 4) and is parallel to the xz-plane and the yz-plane. 14. The line passes through the point (-4, 5, 2) and is parallel to the xy-plane and the yz-plane. 15. The line passes through the point (2, 3, 4) and is perpendicular to the plane given by 3x + 2y - z = 6. 16. The line passes through the point (-4, 5, 2) and is perpendicular to the plane given by - x + 2y + z = 5. 17. The line passes through the point (5, -3, -4) and is parallel to v = (2, - 1, 3). 18. The line passes through the point (-1, 4, -3) and is parallel to v = 5i - j. 19. The line passes through the point (2, 1, 2) and is parallel to the line x = -t, y = 1 + 1,z= -2+1. 20. The line passes through the point (-6, 0, 8) and is parallel to the line x = 5 - 21, y = -4 + 21, z = 0.Determining Parallel Lines In Exercises 25-28, determine whether any of the lines are parallel or identical. 25. L: x = 6 - 3t, y = -2 + 2, z = 5+ 4 Ly: x = 61, y = 2 - 41, z = 13 - 81 Ly: x = 10 - 61, y = 3 + 41. z = 7+ 8 L: x = -4 +61, y = 3 + 41, z = 5 - 6 26. L: x = 3 + 21, y = -61, z = 1 - 2/ L: x = 1 + 2, y= -1 - 1, z= 3 L: x= -1 + 2, y = 3 - 101, z = 1 - 4t L: x = 5 + 21, y= 1 - 1, z= 8 + 31Finding a Point of Intersection In Exercises 29-32, determine whether the lines intersect, and if so, find the point of intersection and the cosine of the angle of intersection. 29. x = 4r + 2, y = 3. z= -1+1 x = 2s + 2, y = 2s +3, z=s+1 30. x = - 3/ + 1, y = 4r + 1, z = 2 + 4 x = 3s + 1, y = 2s + 4. z= -s+ | y = 2 2+3 31. WH =z+1, =y+2= 1 -3 x - 2 2 X-3 32. =z -3. =y+5-2+2 -3 6 2 4