Question: Only question C 2 . 3 . 2 : Find the mistake in the proof - integer division. Theorem: If w , x , y
Only question C
: Find the mistake in the proof integer division.
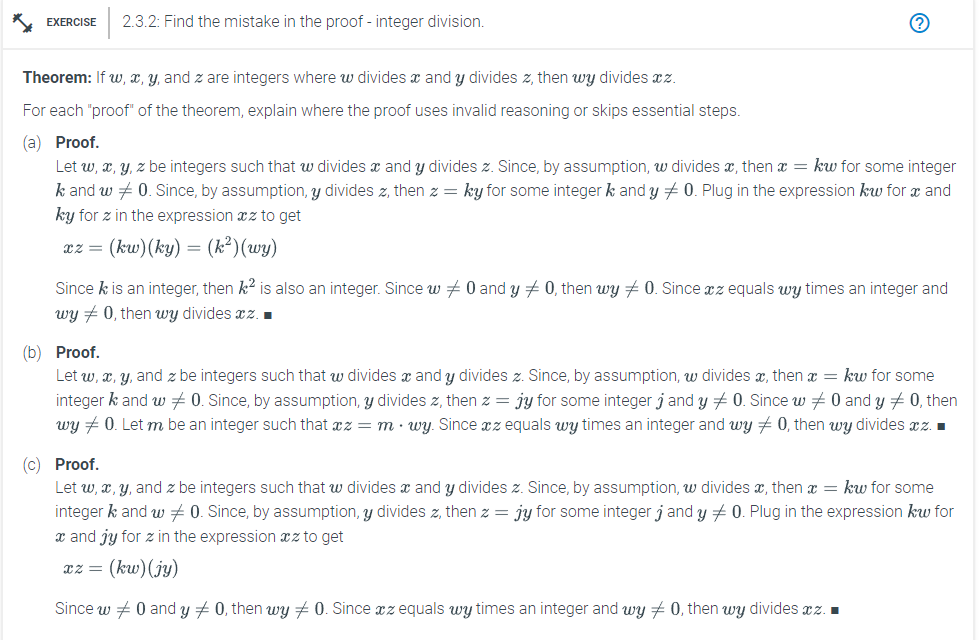
Theorem: If and are integers where divides and divides then divides
For each "proof" of the theorem, explain where the proof uses invalid reasoning or skips essential steps.
a Proof.
Let be integers such that divides and divides Since, by assumption, divides then for some integer
and Since, by assumption, divides then for some integer and Plug in the expression for and
for in the expression to get
Since is an integer, then is also an integer. Since and then Since equals times an integer and
then divides
b Proof.
Let and be integers such that divides and divides Since, by assumption, divides then for some
integer and Since, by assumption, divides then for some integer and Since and then
Let be an integer such that Since equals times an integer and then divides
c Proof.
Let and be integers such that divides and divides Since, by assumption, divides then for some
integer and Since, by assumption, divides then for some integer and Plug in the expression for
and for in the expression to get
Since and then Since equals times an integer and then divides
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


