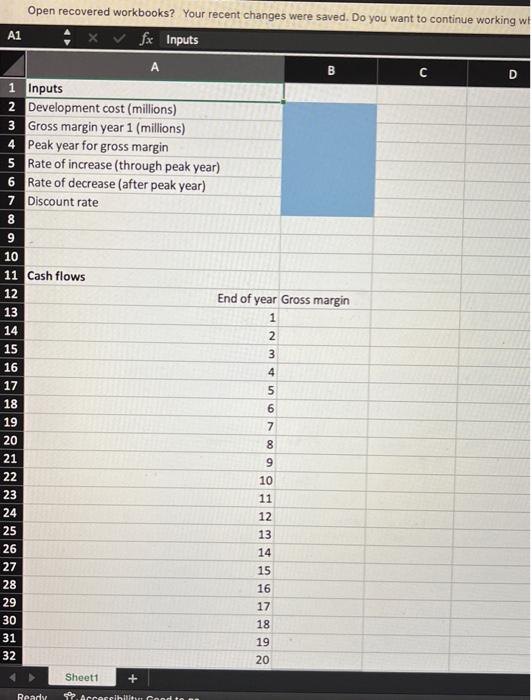
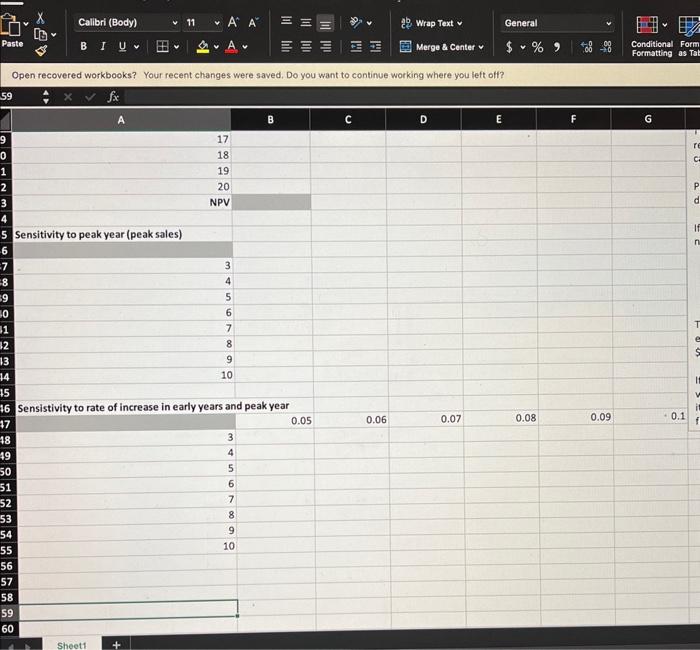
Open recovered workbooks? Your recent changes were saved. Do you want to continue working w Open recovered workbooks? Your recent changes were saved, Do you want to continue working where you left off? 59xfx A B C D E F G \begin{tabular}{|r|} \hline 17 \\ \hline 18 \\ \hline 19 \\ \hline 20 \\ \hline NPV \end{tabular} Sensitivity to peak year (peak sales) Sensistivity to rate of increase in early years and peak year Calculating NPV at Nove Nove is a large drug campany, At the current time, the beginning of year 0. Nove is trying to decide whether one of its new drugs, Niagra, is worth pursuing. Niagra is in the final stages of development and will be ready to enter the market one year from now. The final cost of development, to be incurred at the beginning of year 1, is 515 million. Nove estimates that the demand for Niagra will gradually grow and then decline over its useful lifetime of 20 years. Specifically, the company exprects its gross margin (revenue minus cost) to be 51.5 million in year 1 , then to increase at an annual rate of 6% through year 8 , and finally to decrease at an annual rate of 5A through year 20. Nove wants to develop a spreadsheet model of its 20-year cash flows, assuming its cash flows, other than the initial development cost, are incurred at the end of the reipective years. Using an annual discount rate of 7.5% for the purpose of calculating NPV, the drug company wants to answer the following questions: 1. Is the drug warth pursuing, or should Nove absndon it now and not incur the 515 mallion development eost? 2. How do changes in the model inputs change the answer to question 1 ?. Decision Involving the Time Value of Money In many business situations, cash flows are received at different points in time, and a company must determine a course of action that maximizes the "value" of cash flows. Some examples: - Should a company buy a more expensive machine that lasts for 10 years or a less expensive machine that lasts for 5 years? - What level of plant capacity is best for the next 20 years? Money earned in the future is less valuable than money earned today, for the simple reason that money earned today can be invested to earn returns. Similarly, the costs incurred in the future are less "costly" than costs incurred today. This is why you typically don't simply sum up revenues and costs in a multi-period model. Instead you discount future revenues and costs for a fair comparison with revenues and costs incurred today. The resulting sum of discounted cash flows is the net present value (NPV). Projects with positive NPVs typically increase the value of the company, whereas projects with negative NPVs decrease the value of the company. If money can be invested at a 5%(r=0.05; the rate r is called the discount rate) annual interest rate, then $1 received now is essentially equivalent to $1.05 a year from now. $1.00=$1.05ayearfromnow=$1.00(1+r) Dividing both sides by (1+r) $1.00/(1+r)=$1.00ayearfromnow The value of 1/(1+r) is called the discount factor, and it is always less than 1 . In this example, for r=0.05, it is evaluates to $0.952 and represents the present value of $1.00 received a year from now. The idea is that if you had $0.952 now, you could invest it at 5% and have it grow to $1.00 in a year. If money can be invested at an annual rate r compunded each year, then $1 received t years from now has the same value as 1/(1+r)t dollars received today. If you multiply a cash flow received t years from now by 1/(1+r)t to obtain its present value, the total (sum) of these present values over all years is called the net present value (NPV) of cash flows. Question 1. Which has a greater present value: the gross margin for year 1 or the gross margin for year 8 (the peak year for gross margin)? Answer: Question 2. What is the present value of the gross margin at year 16? Answer: Question 3. What rate of increase ineeded from year 1 through year 8 to have a year 8 gross margin with a present value that is equal to the present value of the year 1 gross margin? Hint: Use goal seek. Answer: Open recovered workbooks? Your recent changes were saved. Do you want to continue working w Open recovered workbooks? Your recent changes were saved, Do you want to continue working where you left off? 59xfx A B C D E F G \begin{tabular}{|r|} \hline 17 \\ \hline 18 \\ \hline 19 \\ \hline 20 \\ \hline NPV \end{tabular} Sensitivity to peak year (peak sales) Sensistivity to rate of increase in early years and peak year Calculating NPV at Nove Nove is a large drug campany, At the current time, the beginning of year 0. Nove is trying to decide whether one of its new drugs, Niagra, is worth pursuing. Niagra is in the final stages of development and will be ready to enter the market one year from now. The final cost of development, to be incurred at the beginning of year 1, is 515 million. Nove estimates that the demand for Niagra will gradually grow and then decline over its useful lifetime of 20 years. Specifically, the company exprects its gross margin (revenue minus cost) to be 51.5 million in year 1 , then to increase at an annual rate of 6% through year 8 , and finally to decrease at an annual rate of 5A through year 20. Nove wants to develop a spreadsheet model of its 20-year cash flows, assuming its cash flows, other than the initial development cost, are incurred at the end of the reipective years. Using an annual discount rate of 7.5% for the purpose of calculating NPV, the drug company wants to answer the following questions: 1. Is the drug warth pursuing, or should Nove absndon it now and not incur the 515 mallion development eost? 2. How do changes in the model inputs change the answer to question 1 ?. Decision Involving the Time Value of Money In many business situations, cash flows are received at different points in time, and a company must determine a course of action that maximizes the "value" of cash flows. Some examples: - Should a company buy a more expensive machine that lasts for 10 years or a less expensive machine that lasts for 5 years? - What level of plant capacity is best for the next 20 years? Money earned in the future is less valuable than money earned today, for the simple reason that money earned today can be invested to earn returns. Similarly, the costs incurred in the future are less "costly" than costs incurred today. This is why you typically don't simply sum up revenues and costs in a multi-period model. Instead you discount future revenues and costs for a fair comparison with revenues and costs incurred today. The resulting sum of discounted cash flows is the net present value (NPV). Projects with positive NPVs typically increase the value of the company, whereas projects with negative NPVs decrease the value of the company. If money can be invested at a 5%(r=0.05; the rate r is called the discount rate) annual interest rate, then $1 received now is essentially equivalent to $1.05 a year from now. $1.00=$1.05ayearfromnow=$1.00(1+r) Dividing both sides by (1+r) $1.00/(1+r)=$1.00ayearfromnow The value of 1/(1+r) is called the discount factor, and it is always less than 1 . In this example, for r=0.05, it is evaluates to $0.952 and represents the present value of $1.00 received a year from now. The idea is that if you had $0.952 now, you could invest it at 5% and have it grow to $1.00 in a year. If money can be invested at an annual rate r compunded each year, then $1 received t years from now has the same value as 1/(1+r)t dollars received today. If you multiply a cash flow received t years from now by 1/(1+r)t to obtain its present value, the total (sum) of these present values over all years is called the net present value (NPV) of cash flows. Question 1. Which has a greater present value: the gross margin for year 1 or the gross margin for year 8 (the peak year for gross margin)? Answer: Question 2. What is the present value of the gross margin at year 16? Answer: Question 3. What rate of increase ineeded from year 1 through year 8 to have a year 8 gross margin with a present value that is equal to the present value of the year 1 gross margin? Hint: Use goal seek