operation research course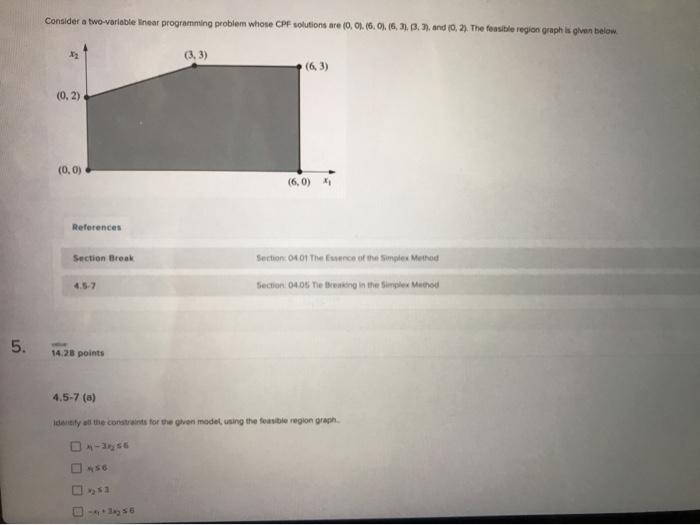

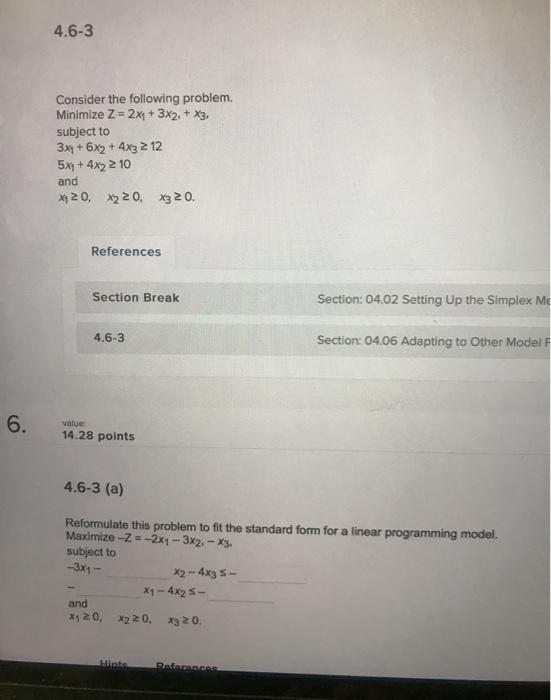
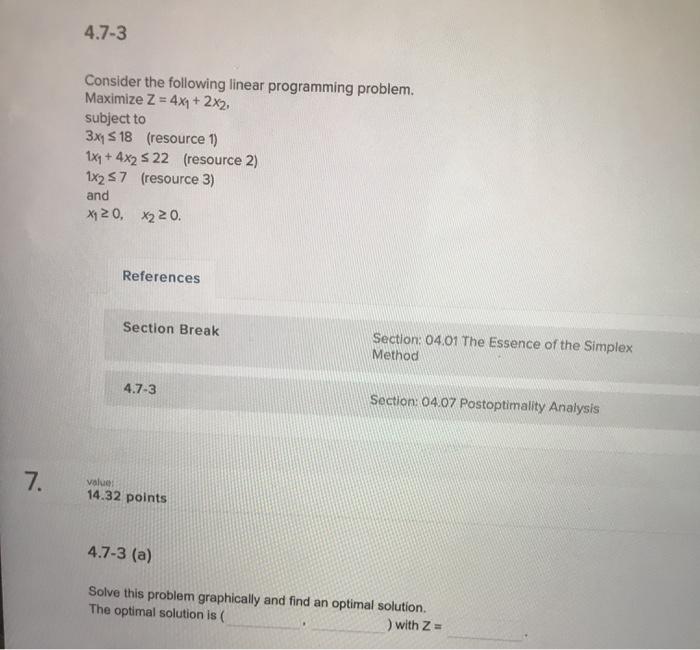
Consider a two-verlable linear programming problem whose CPF solutions are (0,0).(6.0), (6, 31.8., and (0, 2). The feasible region graph is given below (3.3) (0.2) (0,0) (6.0) References Section Break Section Of The Essence of the Suplex Method Section 0405 Teing in the simplex Method LO 14.28 points 4.5-7 (a) Iconly the constraints for the given model, using the fous le region graph 4-6 4.6-3 Consider the following problem. Minimize Z = 2x4 + 3x2, + x3, subject to 3x4 + 6x2 + 4x3 2 12 5x4 + 4x2 2 10 and X420, X220, X3 20. References Section Break Section: 04.02 Setting up the Simplex Me 4.6-3 Section: 04.06 Adapting to Other Model 6. value 14.28 points 4.6-3 (a) Reformulate this problem to fit the standard form for a linear programming model. Maximize -Z = -2x1 - 3x2. - X3. subject to 3x1 x2 - 4x3 5- x - 4x25- and X120, X220. X3 20. Hint Before 4.7-3 Consider the following linear programming problem. Maximize Z = 4x4 + 2x2, subject to 3xy S 18 (resource 1) 1x4 + 4x2 S 22 (resource 2) 1x2 57 (resource 3) and x120, X220. References Section Break Section: 04.01 The Essence of the Simplex Method 4.7-3 Section: 04.07 Postoptimality Analysis 7. value 14.32 points 4.7-3 (a) Solve this problem graphically and find an optimal solution The optimal solution is ( with Z