Optimization in Networks question. Please help me!!!

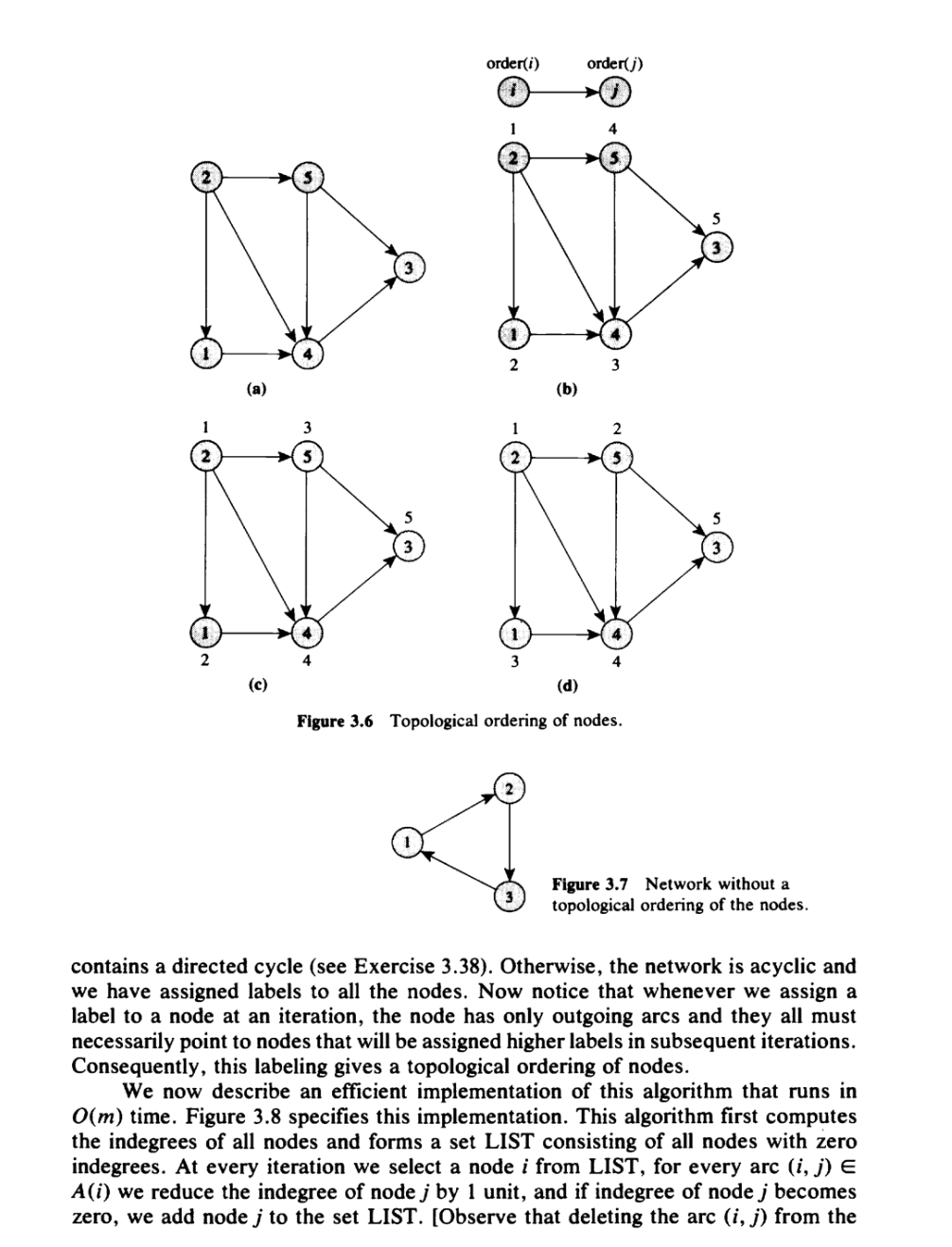
Breadth-First Search If we maintain the set LIST as a queue, we always select nodes from the front of LIST and add them to the rear. In this case the search algorithm selects the marked nodes in a first-in, first-out order. If we define the distance of a node i as the minimum number of arcs in a directed path from node s to node i, this kind of search first marks nodes with distance 1, then those with distance 2, and so on. Therefore, this version of search is called a breadth-first search and the resulting search tree is a breadth-first search tree. Figure 3.5(b) specifies the breadth-first search tree for the network shown in Figure 3.5(a). In subsequent chapters we use the following prop- erty of the breadth-first search tree whose proof is left as an exercise (see Exercise 3.30). Property 3.3. In the breadth-first search tree, the tree path from the source node s to any node i is a shortest path (i.e., contains the fewest number of arcs among all paths joining these two nodes). Depth-First Search If we maintain the set LIST as a stack, we always select the nodes from the front of LIST and also add them to the front. In this case the search algorithm selects the marked node in a last-in, first-out order. This algorithm performs a deep probe, creating a path as long as possible, and backs up one node to initiate a new probe when it can mark no new node from the tip of the path. Consequently, we call this version of search a depth-first search and the resulting tree a depth-first search tree. The depth-first traversal of a network is also called its preorder traversal. Figure 3.5(c) gives the depth-first search tree for the network shown in Figure 3.5(a). In subsequent chapters we use the following property of the depth-first search tree, which can be easily proved using induction arguments (see Exercise 3.32). Property 3.4 (a) If node j is a descendant of node i and j # i, then order(j) > order(i). (b) All the descendants of any node are ordered consecutively in sequence.Topological Ordering Let us label the nodes of a network G = (N. A) by distinct numbers from I through a and represent the labeling by an array order He, orderU) gives the label of node i]. We say that this labeling is a topological ordering of nodes if every arc joins a lower-labeled node to a higher-labeled node. That is. for every are (i, j) E A. order\") order(4). However, the labelings shown in Figure 3.6(c) and (d) are to pological orderings. As shown in this example, a network might have several to- pological orderings. Some networks cannot be topologically ordered. For example, the network shown in Figure 3.7 has no such ordering. This network is cyclic because it contains a directed cycle and for any directed cycle W we can never satisfy the condition order-(i)