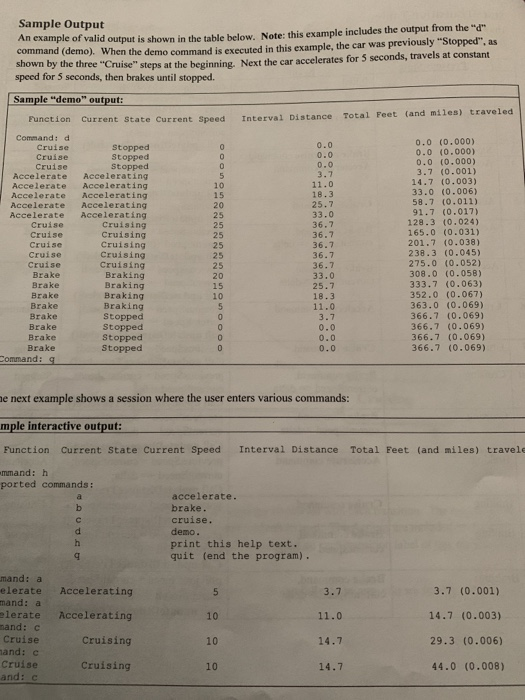
Overview Automobile Speed/Distance Application Program This programming project involves creating a C++ program which distance traveled over a period of time. This should be an interactive program the user and produces text output on the console. Each command entered by the user should execute one interval". For example, the "(accelerate) command should increase the speed by 5 miles per hour (MPH) over simulates the speed of a car and calculates the which accepts keyboard input from interval of I second. Similarly, the "b" (brake) command should decrease the speed by 5 MPH over a time interval of I second, and the "e" (cruise) command should keep the speed constant for I second. All of these perations include calculation of how far the car travels during the 1 second interval, and the total distance since the program started. A separate "d" (demo) command outputs a sequence of steps, similar to that shown in sample data, simply by executing the other operations in a predetermined sequence. Be sure This document discusses the requirements for the program, as well as possible implementation details. you understand this document before you begin coding your final solution. General Discussion of the Project Imagine a car which starts out "Stopped", at some initial position. We could say and its current speed is zero Mil initial position. However, if the driver steps on the gas pedal, the car will "accelerate": its speed will increase some amount. Now that the car is moving, its position will change over time. does nothing, then How much will the position change? This depends on the speed, and how much time has elapsed. It turns out that a car moving at a constant speed of 25 miles per hour (36.7 feet per second) will travel 367 feet in 10 seconds. (Multiply 36.7 feet per second times 10 seconds.) But what if the speed is not constant? In this case we need to know the average speed over the specified time interval. If the speed changes at a constant rate, perhaps 5 miles-per-hour each second, then the average speed i the speed at the beginning of the time interval (previousSpeed), plus the speed at the end of the time interva (currentspeed), divided by2 averageSpeed (previousSpeed + currentSpeed) / 2: averageSpeed FeetPerSecond averageSpeed 5280.0/3600.0 intervalFeetTraveled averageSpeed FeetPerSecond timeInterval; For convenience, we can keep the timeInterval value fixed at one second. The calculations described above mention speed in "miles per hour" and distance in "feet". This is deliberate esthetic reasons: people are accustomed to thinking of the speed of a car in "miles per hour", at least in the United States. Yet, if we were to express the distance traveled over a few seconds in miles, then the numbers would be tiny fractions of a mile, and would therefore not be intuitively appropriate to the person using the program. This is why the averageSpeed value is converted from miles per hour (MPH) to feet per second (FPS). In general, the formula for converting miles per hour (MPH) to feet per second (FPS) is: 5280.0 FPS MPH 3600.0 Possible Program Variables Description These variable names are a suggestion, intended to get you thinking about the problem. The implementation which you choose may be different. The contents of each variable to represent the car could be as follows Variable currentS previousspeed Speed of the car at the end of the "previous" time interval (miles per hour) Description Current speed of the car (miles per hour) totalFeetTraveled intervalFeet Traveled Total feet traveled by the car (since the program started) Total feet traveled during the most recent time interval The amount of elapsed time for each calculation interval (fixed at 1 second) Current state of the car's motion. Valid values are: "Stopped", "Accelerating", "Cruising" (moving at a steady speed), or "Braking The amount which the speed of the car will increase (during acceleration) or decrease (during braking). By default, this value should be 5 miles per hour. timeInterval currentState delta The "accelerate", "brake", and "cruise" operations can be calculated as shown. (In this table, the default value of "delta" is 5 MPH.) Operation accelerate Calculation previousSpeed currentSpeed: currentspeed currentSpeed + delta; PreviousSpeed currentSpeed; currentSpeed currentSpeed - delta; brake cruise previousSpeed-currentSpeed; Design Note: You must write sparate functions for the accelerate, brake, and cruise operations. Not only does this improve the modularity of the program, but it will also make it very easy for you to write the code for the demo operation described later in this document. Possible Function Descriptions Below is a list of possible functions, and their descriptions. Function outputStatusHeader outputStatus Member Function Description Output current data values to the console. totalFeet averageSpeed - (previousSpeed + currentspeed) on the next page). update DistanceTraveled Calculate the intervalFeetTraveled (over e the intervalFeet Traveled (over the most recent calculation interval) and Traveled (since the program started) using the following formula: 2: averagespeed FeetPerSecond averageSpeed 5280.0/3600.0; ntervalFeetTraveled averageSpeed FeetPerSecond timeInterval: totalFeetrraveled - totalFeettraveled intervalFeetTraveled accelerate brake cruise demo Remember to convert Miles-per-hour to feet-per-second before calculating the distance You must write separate functions for accelerate, brake, and eruise. This will make it easier for you to write the code for the demo command. Execute a predetermined sequence of the accelerate, brake, and cruise operations. (See the Sample Output section of this document for one possible sequence.) Some Thoughts about Modeling a Physical System Whenever writing code to simulate the operation of a physical system, keep in mind how the real physical system would behave and try to make your simulation match that behavior as closely as reasonably possible. In this project, this issue comes up when maintaining the "currentState" variable. For example, if the car is currently "Stopped", and the main program executes the "cruise" command, or the "brake" command, then the car should remain "Stopped" Similarly, if the car is moving and the main program executes the "brake" command, then the car should enter the "Braking" state and the speed should decrease. If the main program continues to execute the "brake" command repeatedly, then eventually the speed will reach zero. At this time, the car should transition to the "Stopped state, and the car should remain "Stopped" even if the "brake" command continues to get executed again and again. This is how a real car would behave, so it is how our simulation should hopefully behave. (This is the reason why the State Transition Diagram on the next page has two variations of the "brake" command: "Br is a brake command when the initial speed is greater than the "delta" value. "Bs" is a brake command when the initial speed is less than or equal to the "delta" value. The "delta" value is the amount which the speed changes whenever the accelerate or brake command is used. By default, "delta" should be 5 MPH.) An example of incorrect behavior would be for the car to start moving backwards (speed