package mobiles;

import java.awt.FontMetrics; import java.awt.Graphics2D; import java.awt.geom.AffineTransform; import java.awt.geom.Arc2D; import java.awt.geom.Line2D;

/** * A Mobile is either a Bob or Rod. * * A Bob is a Mobile consists of a weight hanging from a vertical wire. * * Here's a diagram, where W denotes a weight: * *

 * | * W * 

* * A Rod is a Mobile that consists of a horizontal rod that has one Mobile hanging from its left end and another Mobile * hanging from its right end. The rod is hanging from a vertical wire. The distance along the rod from the vertical * wire to the left end is called the left length, and the distance from the vertical wire to the right end is called * the right length. * * Here's a diagram: * *

 * _____|__________ * | | * L R * 

* * The left length is 5 and the right length is 10. L and R are the left and right Mobiles, respectively. */ public class Mobile { /** * True if the Mobile is a Bob; false if the Mobile is a Rod. */ private boolean isBob;

/** * If isBob is true, contains the weight of the Bob. */ private int weight;

/** * If isBob is false, contains the left length of the Rod. */ private int leftLength; /** * If isBob is false, contains the right length of the Rod. */ private int rightLength; /** * If isBob is false, contains the left Mobile of the Rod. */ private Mobile left; /** * If isBob is false, contains the right Mobile of the Rod. */ private Mobile right;

/** * Creates a Bob with the given weight. */ public Mobile (int weight) { this.isBob = true; this.weight = weight; }

/** * Creates a Rod of the given configuration. */ public Mobile (int leftLength, int rightLength, Mobile left, Mobile right) { this.isBob = false; this.leftLength = leftLength; this.left = left; this.rightLength = rightLength; this.right = right; }

// Formatting constants public final static double WIRE = 100; public final static double UNIT = 10; public final static double GAP = 2; public final static double TOP = 10; public final static int WIDTH = 1200; public final static int HEIGHT = 800;

/** * Draws this Mobile on g, beginning at point (x,y). */ public void display (Graphics2D g, double x, double y) { if (isBob) { FontMetrics fm = g.getFontMetrics(); int weightWidth = fm.stringWidth(weight + ""); int height = fm.getHeight(); g.draw(new Line2D.Double(x, y, x, y + WIRE)); g.draw(new Arc2D.Double(x - height, y + WIRE, 2 * height, 2 * height, 0, 360, Arc2D.OPEN)); g.drawString(weight + "", (float) (x - weightWidth / 2), (float) (y + WIRE + 1.25 * height)); }

else { // Get the widths of the labels FontMetrics fm = g.getFontMetrics(); int leftLabelWidth = fm.stringWidth(leftLength + ""); int rightLabelWidth = fm.stringWidth(rightLength + "");

// Show the mobile askew according to the degree of imbalance double leftTorque = left.weight() * leftLength; double rightTorque = right.weight() * rightLength; double theta = (rightTorque - leftTorque) / 100 * Math.PI / 6; theta = Math.min(theta, Math.PI / 6); theta = Math.max(theta, -Math.PI / 6);

// Compute the endpoints of the rod double leftX = x - Math.cos(theta) * (leftLength * UNIT); double leftY = y + WIRE - Math.sin(theta) * (leftLength * UNIT); double rightX = x + Math.cos(theta) * (rightLength * UNIT); double rightY = y + WIRE + Math.sin(theta) * (rightLength * UNIT);

// Translate AffineTransform at = new AffineTransform(); at.translate(x, y + WIRE); g.setTransform(at); // Draw the wire g.draw(new Line2D.Double(0, 0, 0, -WIRE)); // Rotate at.rotate(theta); g.setTransform(at);

// Draw the rod and display the text g.draw(new Line2D.Double(-leftLength * UNIT, 0, rightLength * UNIT, 0)); g.drawString(leftLength + "", (float) (-leftLength * UNIT / 2 - leftLabelWidth / 2), (float) -GAP); g.drawString(rightLength + "", (float) (rightLength * UNIT / 2 - rightLabelWidth / 2), (float) -GAP);

// Cancel the rotation at.setToRotation(0); g.setTransform(at);

// Display the left and right Mobiles left.display(g, leftX, leftY); right.display(g, rightX, rightY); } }

/** * Returns the total weight of all the Bobs in this Mobile. */ public int weight () { return 0; }

/** * Reports whether all the Rods in this Mobile are completely horizontal. A Rod will be horizontal if the product of * its left length and the weight of its left Mobile equals the product of its right length and the weight of its * right Mobile. */ public boolean isBalanced () { return false; }

/** * Returns the length of the longest path through this Mobile. There is one path for every Bob in the Mobile. Each * path leads from the top of the Mobile to a Bob, and its length is the number of Rods encountered along the way * plus one. */ public int depth () { return 0; }

/** * Returns the number of Bobs contained in this Mobile. */ public int bobCount () { return 0; }

/** * Returns the number of Rods contained in this Mobile. */ public int rodCount () { return 0; }

/** * Returns the length of the longest Rod contained in this Mobile. If there are no Rods, returns zero. */ public int longestRod () { return 0; }

/** * Returns the weight of the heaviest Bob contained in this Mobile. */ public int heaviestBob () { return 0; } }

Example Mobiles

package mobiles;

import javax.swing.SwingUtilities;

public class MobileExamples

{

public static void main (String[] args)

{

SwingUtilities.invokeLater( () -> new MobileViewer(makeMobile1(), "Mobile 1"));

}

public static Mobile makeMobile1 ()

{

Mobile m6 = new Mobile(28, 7, new Mobile(10), new Mobile(40));

Mobile m5 = new Mobile(12, 18, new Mobile(3), new Mobile(2));

Mobile m4 = new Mobile(5, 20, new Mobile(20), m5);

Mobile m3 = new Mobile(24, 12, m4, new Mobile(50));

Mobile m2 = new Mobile(30, 10, new Mobile(25), m3);

Mobile m1 = new Mobile(20, 40, m2, m6);

return m1;

}

public static Mobile makeMobile2 ()

{

Mobile m6 = new Mobile(28, 7, new Mobile(10), new Mobile(40));

Mobile m5 = new Mobile(10, 20, new Mobile(3), new Mobile(2));

Mobile m4 = new Mobile(5, 20, new Mobile(20), m5);

Mobile m3 = new Mobile(24, 12, m4, new Mobile(50));

Mobile m2 = new Mobile(30, 10, new Mobile(25), m3);

Mobile m1 = new Mobile(20, 40, m2, m6);

return m1;

}

public static Mobile makeMobile3 ()

{

Mobile m6 = new Mobile(28, 7, new Mobile(10), new Mobile(40));

Mobile m5 = new Mobile(12, 18, new Mobile(3), new Mobile(2));

Mobile m4 = new Mobile(5, 20, new Mobile(20), m5);

Mobile m3 = new Mobile(24, 12, m4, new Mobile(50));

Mobile m2 = new Mobile(29, 10, new Mobile(25), m3);

Mobile m1 = new Mobile(20, 40, m2, m6);

return m1;

}

}

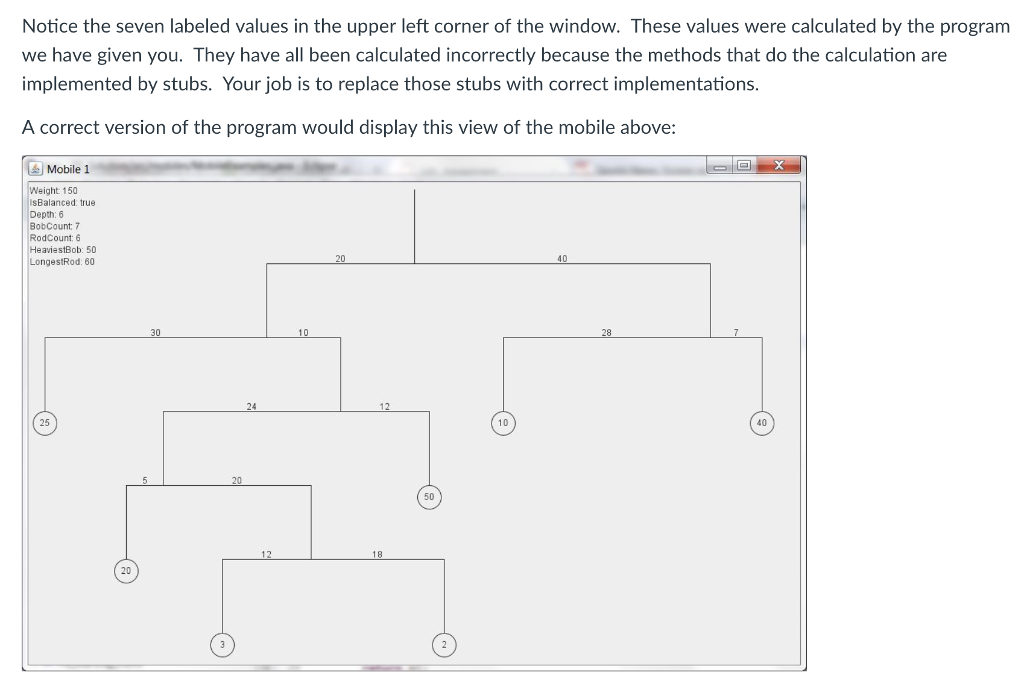
Notice the seven labeled values in the upper left corner of the window. These values were calculated by the program we have given you. They have all been calculated incorrectly because the methods that do the calculation are implemented by stubs. Your job is to replace those stubs with correct implementations. A correct version of the program would display this view of the mobile above: Mobile 1 Weight 150 sBalanced. true Depth: 6 BobCount: 7 RodCount: 6 HeaviestBob: 50 LongestRod: 60 20 40 30 25 40 50 12 20 Notice the seven labeled values in the upper left corner of the window. These values were calculated by the program we have given you. They have all been calculated incorrectly because the methods that do the calculation are implemented by stubs. Your job is to replace those stubs with correct implementations. A correct version of the program would display this view of the mobile above: Mobile 1 Weight 150 sBalanced. true Depth: 6 BobCount: 7 RodCount: 6 HeaviestBob: 50 LongestRod: 60 20 40 30 25 40 50 12 20