Page 36 reference:

Page 44 reference:

Please explain the answer as much as you can and with full step.

(A) part of the question if needed: https://www.chegg.com/homework-help/questions-and-answers/page-18-17-shortest-path-17c-dijkstra-worked-example-page-36-17-shortest-path-page-44-17-s-q50642746?trackid=5p6MiAvu

(i) and (ii) are the subquestion under part (B), they are one question

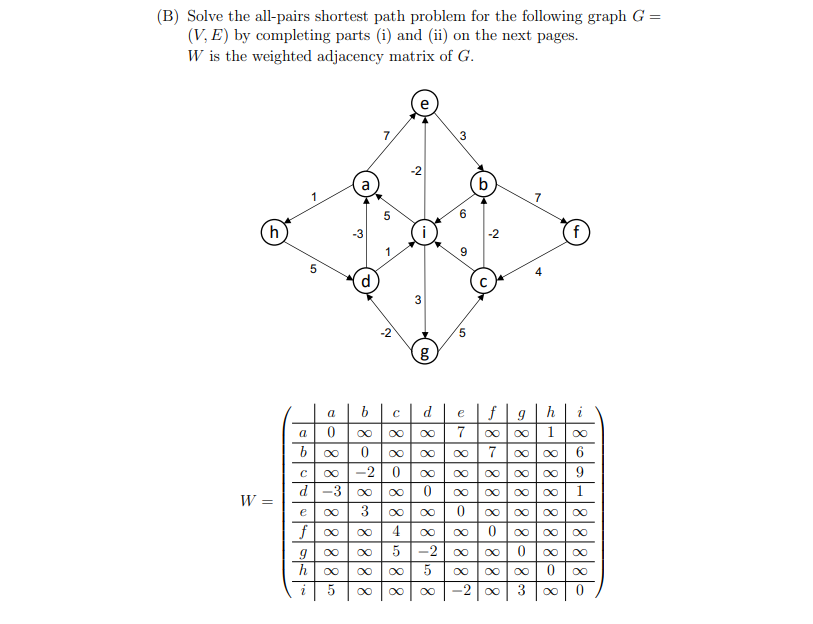
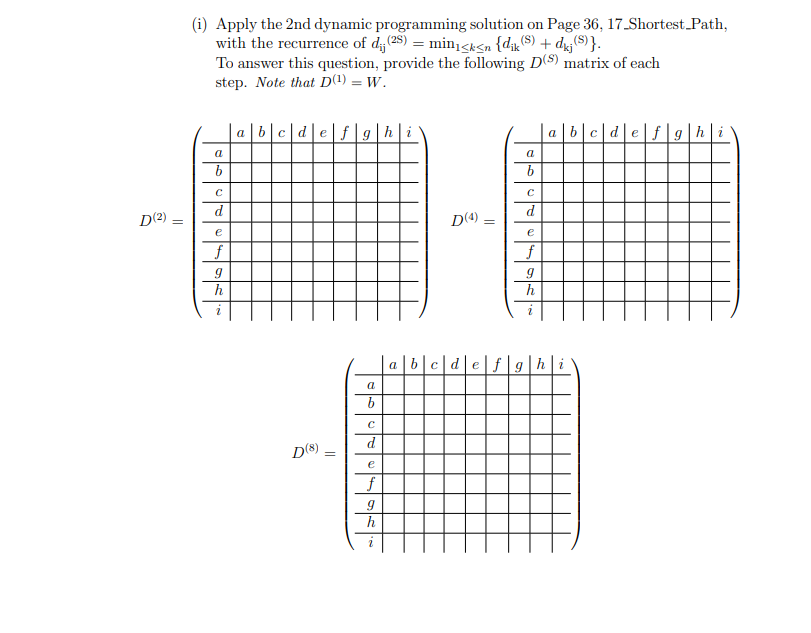
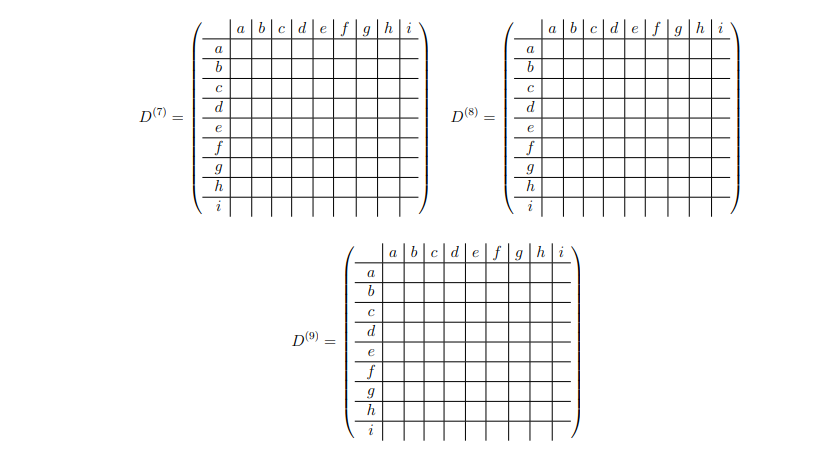
(B) Solve the all-pairs shortest path problem for the following graph G = (V, E) by completing parts (i) and (ii) on the next pages. W is the weighted adjacency matrix of G. 3 2 b 7 5 h -3 -2 f 1 9 5 3 2 5 8 d e f g h i 7 00 01 00 00 00 W e 88 88-80-8 888888 81818 181818 0 00 00 0 000 000 81-888888 8888 9 h 00 00 2 5 00 -200 3 0 (i) Apply the 2nd dynamic programming solution on Page 36, 17 Shortest Path, with the recurrence of d; (25) = min sksn {dik(S) + dk;(S)}. To answer this question, provide the following D(S) matrix of each step. Note that D(1) =W. a b c d e f g h i a b c d e f g h i a a b b d d D(2) D(4) e e 9 h 9 h i 2 abcdefghi a b d D(8) e f 9 h 2 (ii) Apply the Floyd-Warshall algorithm on Page 44, 17 Shortest Path, with the recurrence of d; (k) = min sksn {d; (k-1), dik (k-1) + dx;(k-1)}. To answer this question, provide the D(k) matrix of each step. Note that DO) = W. abcdefghi a b c d e f g h i a b a b d d D(1) D(2) e f 9 h e f g h abcdefghi a b c d e f g h i a a b d d D(3) D e f 9 h e f 9 h abcdefghi a a b c d e f g h i a a b b D(5) = D(6) d e f 9 h d e f 9 h abc d elf 9 h abcdef ghi a a b b d d D(7) D(8) II e f e f 9 h 9 h a b c d e f ghi a b d D(9) e f 9 h Dynamic Programming: Solution 2 Observation: To compute dm), instead of looking at the last stop before j, we look at the middle point. This cuts down the problem size by half. New recurrence: = min {deo + de 1 (28) ij 1skan Algorithm: Calculate D(1), D(2),D(4),D(8), ... Calculating each matrix takes O(n) time: total time = 0(nlogn). Q: This might overshoot D(n-1). Is algorithm still correct? A: It's OK. D(ni), n'> n 1, contains length of shortest paths with at most n' edges; it will not miss any shortest path with up to n - 1 edges. Actually, D(n') D(n-1) for any n' > n - 1, since no shortest path has more than n - 1 edges. . 36 The Floyd-Warshall Algorithm Floyd-Warshall (G): do = w(i,j) for all 1sijsn for k=1 to n let D(k) be a new nxn matrix for i=1 to n for j=1 to n if d -1) + de in (k-1) (k-1) (k-1) (k-1) n 1, contains length of shortest paths with at most n' edges; it will not miss any shortest path with up to n - 1 edges. Actually, D(n') D(n-1) for any n' > n - 1, since no shortest path has more than n - 1 edges. . 36 The Floyd-Warshall Algorithm Floyd-Warshall (G): do = w(i,j) for all 1sijsn for k=1 to n let D(k) be a new nxn matrix for i=1 to n for j=1 to n if d -1) + de in (k-1) (k-1) (k-1) (k-1)