Question: % - - - Parameters a = 1 0 ; % Mesh width p = 0 . 2 5 ; % Link probability % -
Parameters
a ; Mesh width
p ; Link probability
Hexagonal mesh
X Y meshgrid:a:a;
for i ::a
Xi :) Xi :) ; Correcting the offset for even rows
end
Y Y sqrt;
x X:;
y Y:;
Random network generation
Get delaunay triangulation
T delaunayx y;
Get a list of all links
tmp T: T:; T: T:; T: T:;
Filter out duplicates
links uniquemintmp: tmp: maxtmp: tmp: 'rows';
Filter with probability p to get the random network
L linksrandsizelinks p :;
Get sparse adjacency matrix
A sparseL: L: onessizeL a a;
Find clusters using the custom rcm method
tic;
C clustercustomrcmA;
toc;
Display clusters
figure;
hold on;
colors linesnumelC; Generate distinct colors for each cluster
for i :numelC
scatterxCi yCi 'filled', 'MarkerFaceColor', colorsi:;
end
titleClusters found using custom Kmeans method';
xlabelX;
ylabelY;
axis equal;
grid on; Optional: add grid for better visualization
this is the matlab script
this is the matlab function:
function C clustercustomrcmA
Symmetrize adjacency matrix
S A A;
Reverse CuthillMcKee ordering using your custom method
r ReverseCuthillMckeeS;
Get the clusters
C r;
for i :numelr
if anySCend ri
Cendend ri;
else
Cend ri;
end
end
like this create a custom kmeans function that creates clusters using kmeans clustering algorithm instead of reverse cuthill mckee algorithm
the output should look like the image attached but instead of reverse cuthill mckee algorithm for clustering use Kmeans
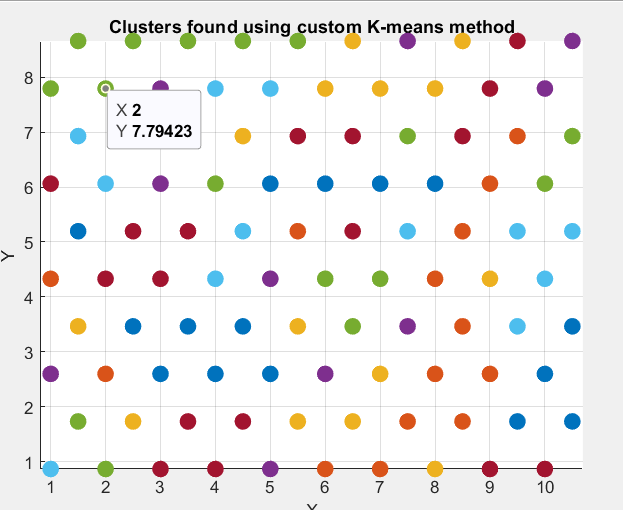
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


