Parametric equations and polar coordinates problem:

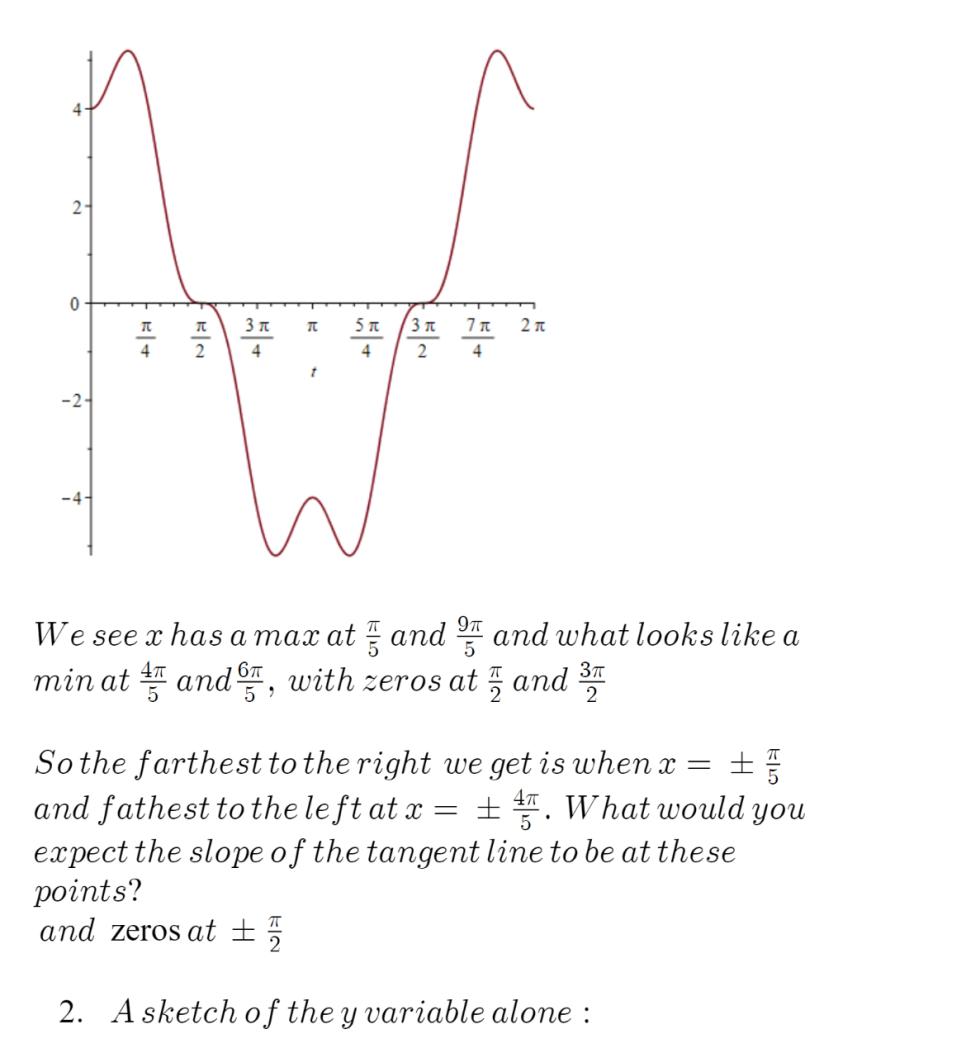
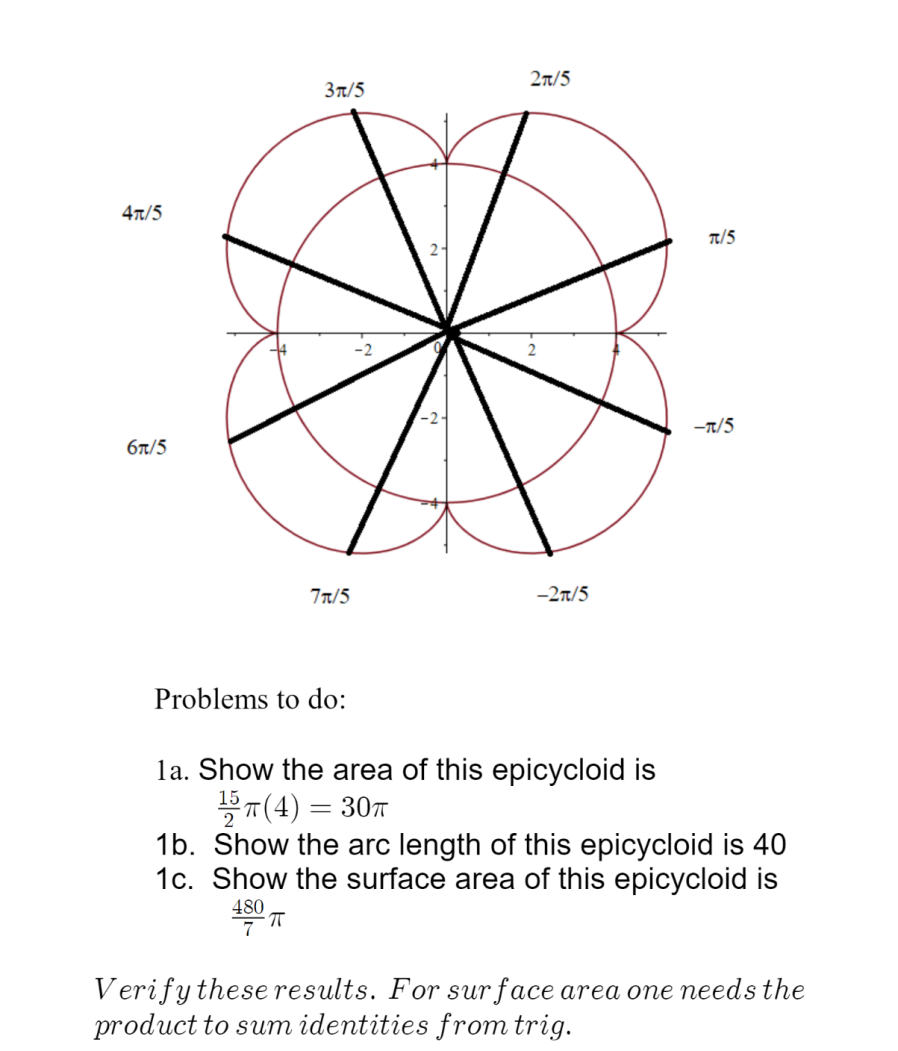
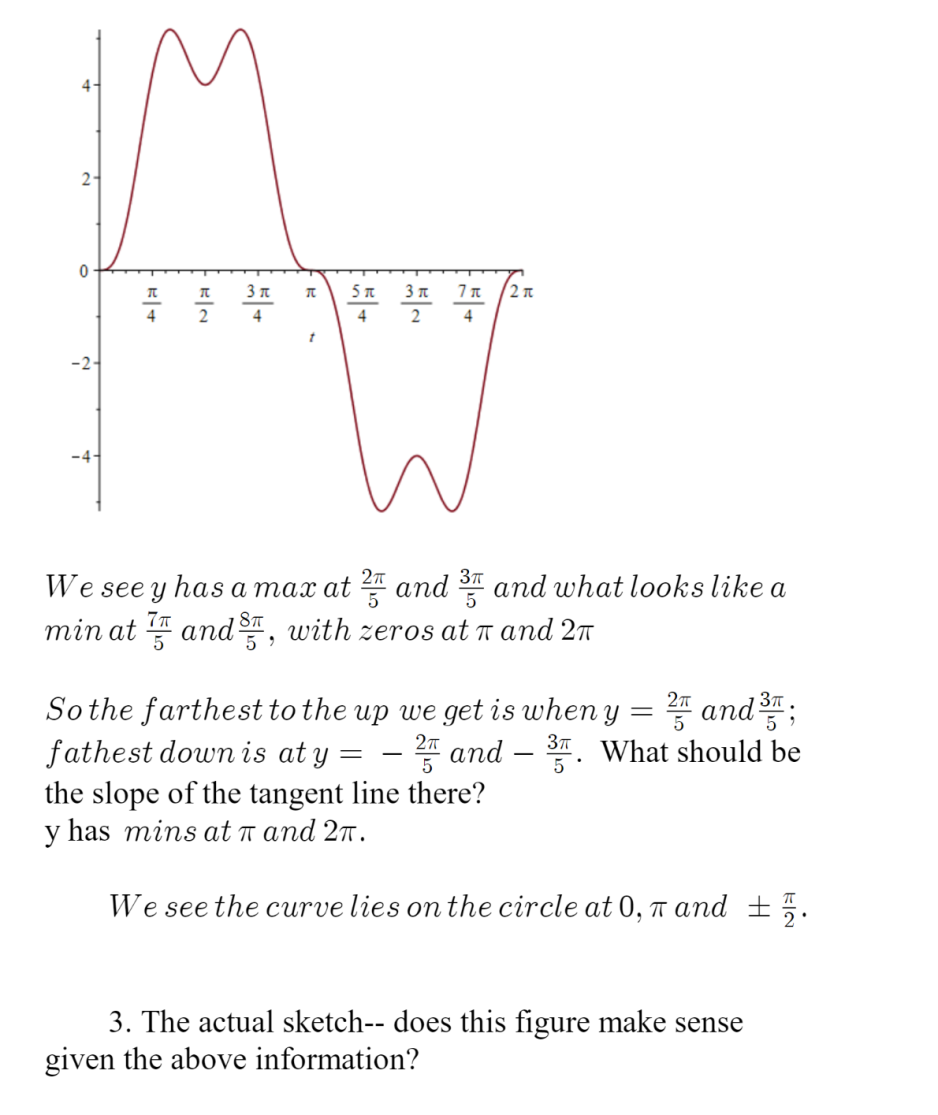
2. Based on the hypocycloid example done June 1, 2020 Topic: the epicycloid; in this case, the 4-cusped epicycloid. We cannot use the chart method for this figure because the parametric equations are more complicated. They are x = 5cos0 - cos50, y = 5sino - sin50 with x = - 5sino + 5sin50 y' = 5cos0 - 5cos50 Helps in sketching the 4 - cusped epicycloid 1. A sketch of the x variable alone :We see x has a mast: at g and 9?\" and what looks like a min at 4% and%\4m'5 Problems to do: la. Show the area of this epicycloid is 1251114) : 307T 1b. Show the arc length of this epicycloid is 40 10. Show the surface area of this epicycloid is 480 7 7T Verify these results. For surface area one needs the product to sum identities from trig. We see y has a max at 2?\" and 3?\" and what looks like a min at % andi, with zeros at it and 277 So the farthest to the up we get is when y Hand 3'\"; fathest down' is at y 2\" and 35 . What should be the slope of the tangent line there? y has mine at 7r and 2%. We see the curve lies on the circle at 0, 7t and :t g 3. The actual sketch-- does this gure make sense given the above information