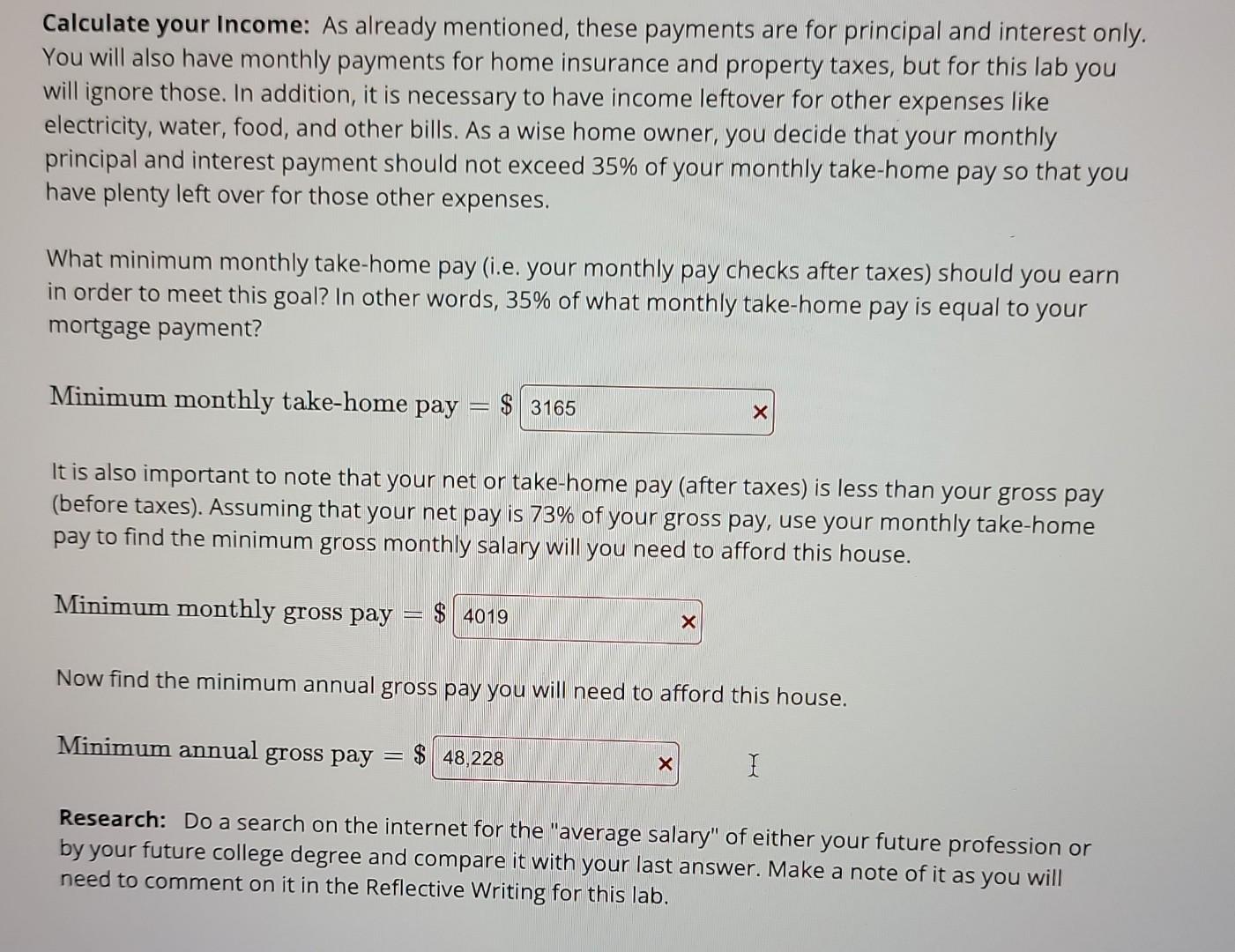
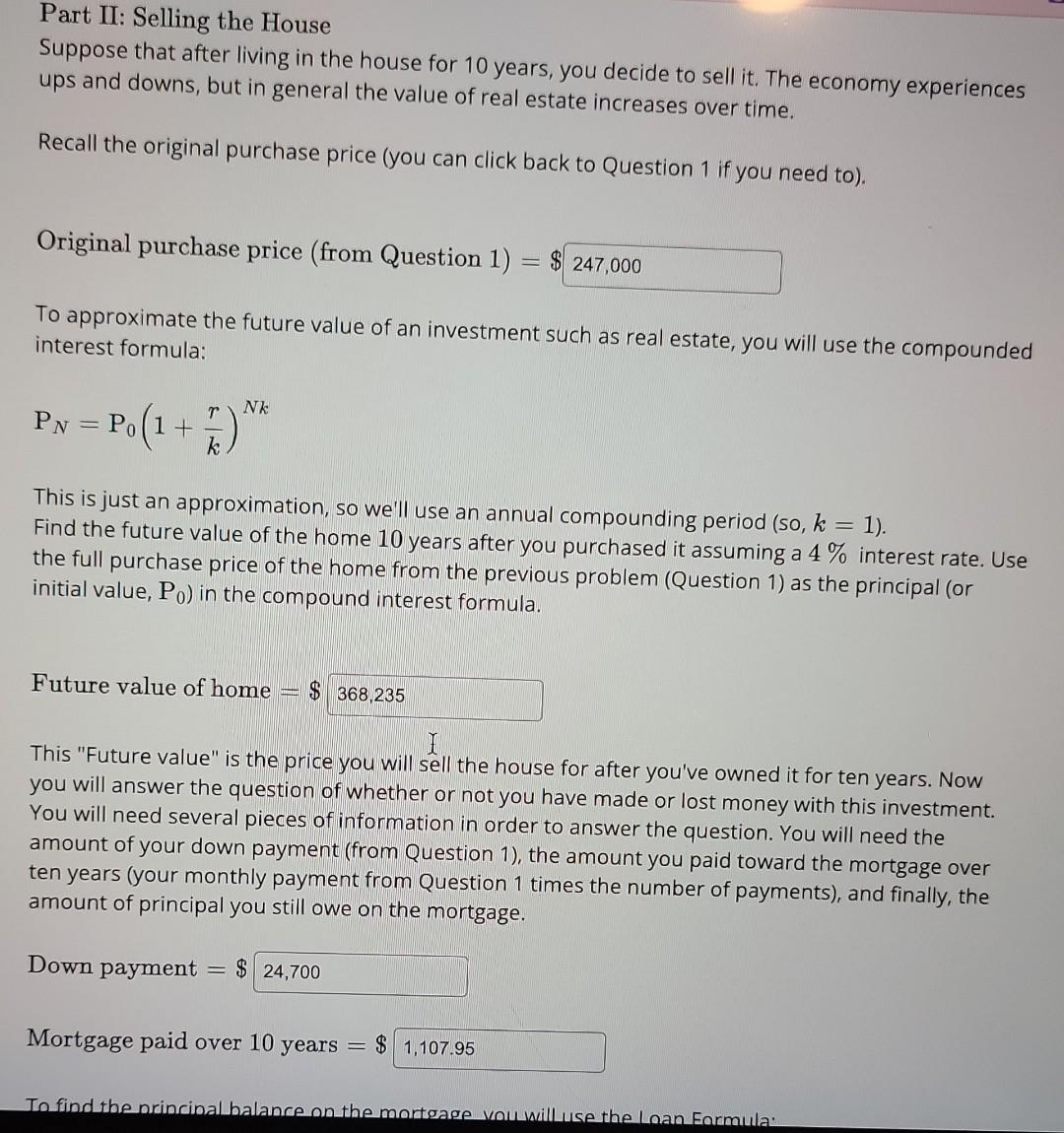
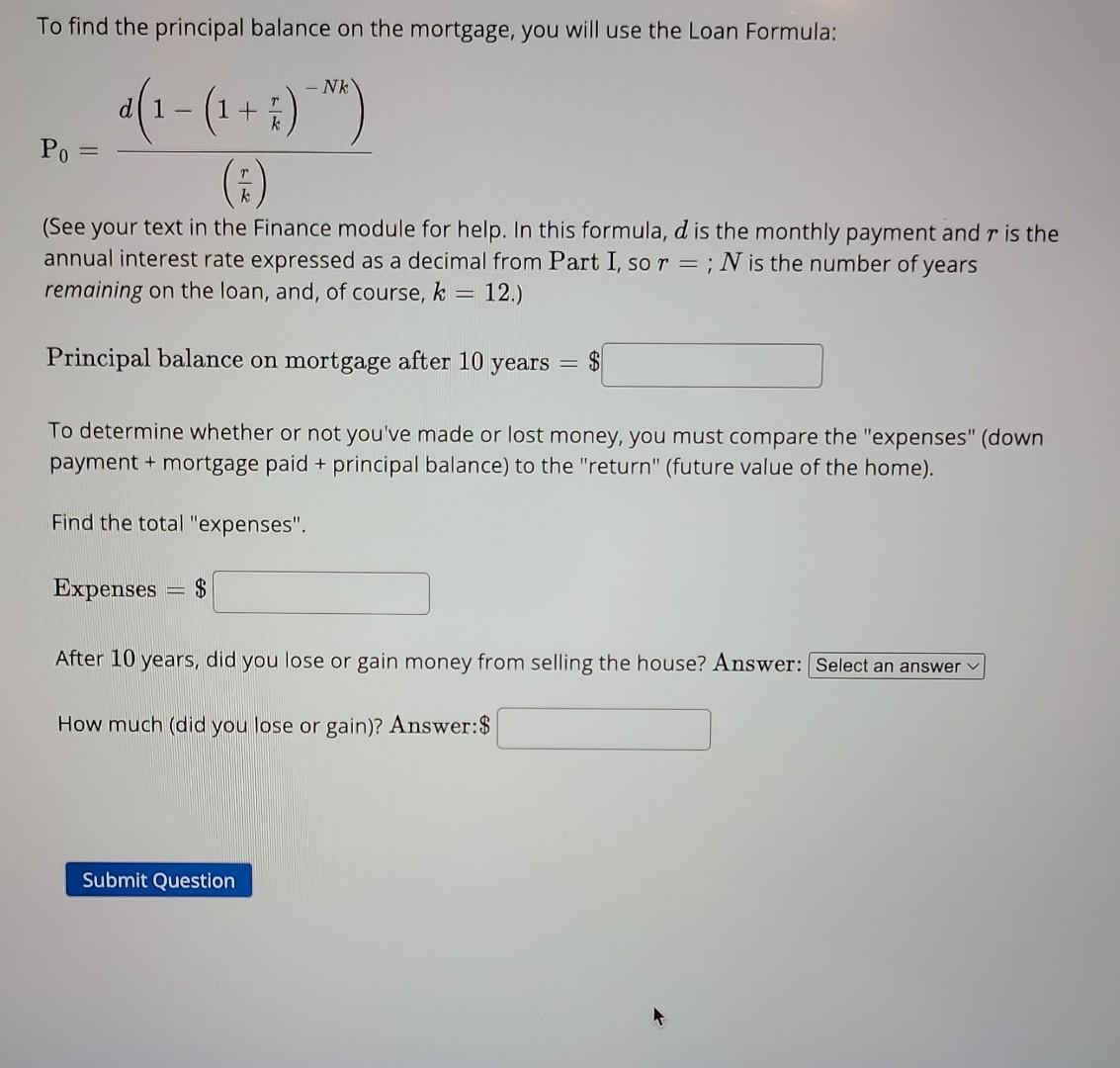
Part 1 & 2.

Introduction: In this lab you will examine a home loan, also known as a mortgage. In Part I you will be computing various values associated with a 30 year loan. In Part II you will calculate values associated with selling the house after 10 years. In Part III you will be computing values associated with a 15 year loan and compare them to the 30 year loan values. In Part IV you will examine the effects of making extra monthly payments on the 30 year loan. In Part V you will do a "Reflective Writing" that will accompany the lab and be submitted with the lab on your e-Portfolio. Warning! You can submit answers to make sure they are correct before proceeding to the next. It is a good idea to also keep a written account of the given values (e.g. original price of the house, annual interest rate, etc.) as you will be asked to refer back to these values as you go. Once you have "submitted" an answer to a question, you can click back and forth between the parts if you need to, though you may need to click on "Reattempt this question" at the top of the page. Don't worry, your correct answers will be saved! Round all of your answers to the nearest cent when appropriate to do so. Some questions are programmed to allow for slight variations in the answers due to rounding errors, BUT it is important that you don't round values you are using in formulas. Only round your final answers. Part I Assume that you have found a home for sale and have agreed to a purchase price of $247000. Down Payment: Assume that you are going to make a 10% down payment on the house. Determine the amount of your down payment and the balance to finance. Down Payment =$ Loan Amount =$ Monthly Payment: Calculate the monthly payment for a 30 year loan (rounding to the nearest cent, so rounding to two decimal places). For the 30 year loan use an annual interest rate of 4.36%. First, express the annual interest rate as a decimal. Monthly Payment: Calculate the monthly payment for a 30 year loan (rounding to the nearest cent, so rounding to two decimal places). For the 30 year loan use an annual interest rate of 4.36%. First, express the annual interest rate as a decimal. The annual interest rate expressed as a decimal is Now use the loan formula to find the monthly payment, d. The loan formula solved for d is: d=(1(1+kr)Nk)P0(kr) P0 is the original loan amount. r is the annual interest rate in decimal form. k is the number of compounding periods in one year (so k=12 ). N is the length of the loan in years. Monthly Payment: d=$ Assuming you make the monthly payment each month for 30 years, what will be the total amount repaid? Total payments =$ Find the total amount of interest paid over the 30 years. To do so, subtract the amount originally borrowed from the total payments. Total interest paid =$ Calculate your Income: As already mentioned, these payments are for principal and interest only. You will also have monthly payments for home insurance and property taxes, but for this lab you will ignore those. In addition, it is necessary to have income leftover for other expenses like electricity, water, food, and other bills. As a wise home owner, you decide that your monthly Calculate your Income: As already mentioned, these payments are for principal and interest only. You will also have monthly payments for home insurance and property taxes, but for this lab you will ignore those. In addition, it is necessary to have income leftover for other expenses like electricity, water, food, and other bills. As a wise home owner, you decide that your monthly principal and interest payment should not exceed 35% of your monthly take-home pay so that you have plenty left over for those other expenses. What minimum monthly take-home pay (i.e. your monthly pay checks after taxes) should you earn in order to meet this goal? In other words, 35% of what monthly take-home pay is equal to your mortgage payment? Minimum monthly take-home pay =$ It is also important to note that your net or take-home pay (after taxes) is less than your gross pay (before taxes). Assuming that your net pay is 73% of your gross pay, use your monthly take-home pay to find the minimum gross monthly salary will you need to afford this house. Minimum monthly gross pay =$ Now find the minimum annual gross pay you will need to afford this house. Minimum annual gross pay =$ Research: Do a search on the internet for the "average salary" of either your future profession or by your future college degree and compare it with your last answer. Make a note of it as you will need to comment on it in the Reflective Writing for this lab. Part II: Selling the House Suppose that after living in the house for 10 years, you decide to sell it. The economy experiences ups and downs, but in general the value of real estate increases over time. Recall the original purchase price (you can click back to Question 1 if you need to). Original purchase price (from Question 1 ) =$ To approximate the future value of an investment such as real estate, you will use the compounded interest formula: PN=P0(1+kr)Nk This is just an approximation, so we'll use an annual compounding period (so, k=1 ). Find the future value of the home 10 years after you purchased it assuming a 4% interest rate. Use the full purchase price of the home from the previous problem (Question 1) as the principal (or initial value, P0 ) in the compound interest formula. Future value of home =$ This "Future value" is the price you will sell the house for after you've owned it for ten years. Now you will answer the question of whether or not you have made or lost money with this investment. You will need several pieces of information in order to answer the question. You will need the amount of your down payment (from Question 1), the amount you paid toward the mortgage over ten years (your monthly payment from Question 1 times the number of payments), and finally, the amount of principal you still owe on the mortgage. Down payment =$ Mortgage paid over 10 years =$ To find the principal balance on the mortgage, you will use the Loan Formula: P0=(kr)d(1(1+kr)Nk) (See your text in the Finance module for help. In this formula, d is the monthly payment and r is the annual interest rate expressed as a decimal from Part I, so r=;N is the number of years remaining on the loan, and, of course, k=12.) Principal balance on mortgage after 10 years =$ To determine whether or not you've made or lost money, you must compare the "expenses" (down payment + mortgage paid + principal balance) to the "return" (future value of the home). Find the total "expenses". Expenses =$ After 10 years, did you lose or gain money from selling the house? Answer: How much (did you lose or gain)? Answer: Introduction: In this lab you will examine a home loan, also known as a mortgage. In Part I you will be computing various values associated with a 30 year loan. In Part II you will calculate values associated with selling the house after 10 years. In Part III you will be computing values associated with a 15 year loan and compare them to the 30 year loan values. In Part IV you will examine the effects of making extra monthly payments on the 30 year loan. In Part V you will do a "Reflective Writing" that will accompany the lab and be submitted with the lab on your e-Portfolio. Warning! You can submit answers to make sure they are correct before proceeding to the next. It is a good idea to also keep a written account of the given values (e.g. original price of the house, annual interest rate, etc.) as you will be asked to refer back to these values as you go. Once you have "submitted" an answer to a question, you can click back and forth between the parts if you need to, though you may need to click on "Reattempt this question" at the top of the page. Don't worry, your correct answers will be saved! Round all of your answers to the nearest cent when appropriate to do so. Some questions are programmed to allow for slight variations in the answers due to rounding errors, BUT it is important that you don't round values you are using in formulas. Only round your final answers. Part I Assume that you have found a home for sale and have agreed to a purchase price of $247000. Down Payment: Assume that you are going to make a 10% down payment on the house. Determine the amount of your down payment and the balance to finance. Down Payment =$ Loan Amount =$ Monthly Payment: Calculate the monthly payment for a 30 year loan (rounding to the nearest cent, so rounding to two decimal places). For the 30 year loan use an annual interest rate of 4.36%. First, express the annual interest rate as a decimal. Monthly Payment: Calculate the monthly payment for a 30 year loan (rounding to the nearest cent, so rounding to two decimal places). For the 30 year loan use an annual interest rate of 4.36%. First, express the annual interest rate as a decimal. The annual interest rate expressed as a decimal is Now use the loan formula to find the monthly payment, d. The loan formula solved for d is: d=(1(1+kr)Nk)P0(kr) P0 is the original loan amount. r is the annual interest rate in decimal form. k is the number of compounding periods in one year (so k=12 ). N is the length of the loan in years. Monthly Payment: d=$ Assuming you make the monthly payment each month for 30 years, what will be the total amount repaid? Total payments =$ Find the total amount of interest paid over the 30 years. To do so, subtract the amount originally borrowed from the total payments. Total interest paid =$ Calculate your Income: As already mentioned, these payments are for principal and interest only. You will also have monthly payments for home insurance and property taxes, but for this lab you will ignore those. In addition, it is necessary to have income leftover for other expenses like electricity, water, food, and other bills. As a wise home owner, you decide that your monthly Calculate your Income: As already mentioned, these payments are for principal and interest only. You will also have monthly payments for home insurance and property taxes, but for this lab you will ignore those. In addition, it is necessary to have income leftover for other expenses like electricity, water, food, and other bills. As a wise home owner, you decide that your monthly principal and interest payment should not exceed 35% of your monthly take-home pay so that you have plenty left over for those other expenses. What minimum monthly take-home pay (i.e. your monthly pay checks after taxes) should you earn in order to meet this goal? In other words, 35% of what monthly take-home pay is equal to your mortgage payment? Minimum monthly take-home pay =$ It is also important to note that your net or take-home pay (after taxes) is less than your gross pay (before taxes). Assuming that your net pay is 73% of your gross pay, use your monthly take-home pay to find the minimum gross monthly salary will you need to afford this house. Minimum monthly gross pay =$ Now find the minimum annual gross pay you will need to afford this house. Minimum annual gross pay =$ Research: Do a search on the internet for the "average salary" of either your future profession or by your future college degree and compare it with your last answer. Make a note of it as you will need to comment on it in the Reflective Writing for this lab. Part II: Selling the House Suppose that after living in the house for 10 years, you decide to sell it. The economy experiences ups and downs, but in general the value of real estate increases over time. Recall the original purchase price (you can click back to Question 1 if you need to). Original purchase price (from Question 1 ) =$ To approximate the future value of an investment such as real estate, you will use the compounded interest formula: PN=P0(1+kr)Nk This is just an approximation, so we'll use an annual compounding period (so, k=1 ). Find the future value of the home 10 years after you purchased it assuming a 4% interest rate. Use the full purchase price of the home from the previous problem (Question 1) as the principal (or initial value, P0 ) in the compound interest formula. Future value of home =$ This "Future value" is the price you will sell the house for after you've owned it for ten years. Now you will answer the question of whether or not you have made or lost money with this investment. You will need several pieces of information in order to answer the question. You will need the amount of your down payment (from Question 1), the amount you paid toward the mortgage over ten years (your monthly payment from Question 1 times the number of payments), and finally, the amount of principal you still owe on the mortgage. Down payment =$ Mortgage paid over 10 years =$ To find the principal balance on the mortgage, you will use the Loan Formula: P0=(kr)d(1(1+kr)Nk) (See your text in the Finance module for help. In this formula, d is the monthly payment and r is the annual interest rate expressed as a decimal from Part I, so r=;N is the number of years remaining on the loan, and, of course, k=12.) Principal balance on mortgage after 10 years =$ To determine whether or not you've made or lost money, you must compare the "expenses" (down payment + mortgage paid + principal balance) to the "return" (future value of the home). Find the total "expenses". Expenses =$ After 10 years, did you lose or gain money from selling the house? Answer: How much (did you lose or gain)