Part 2 please question 1 and 2 with work.

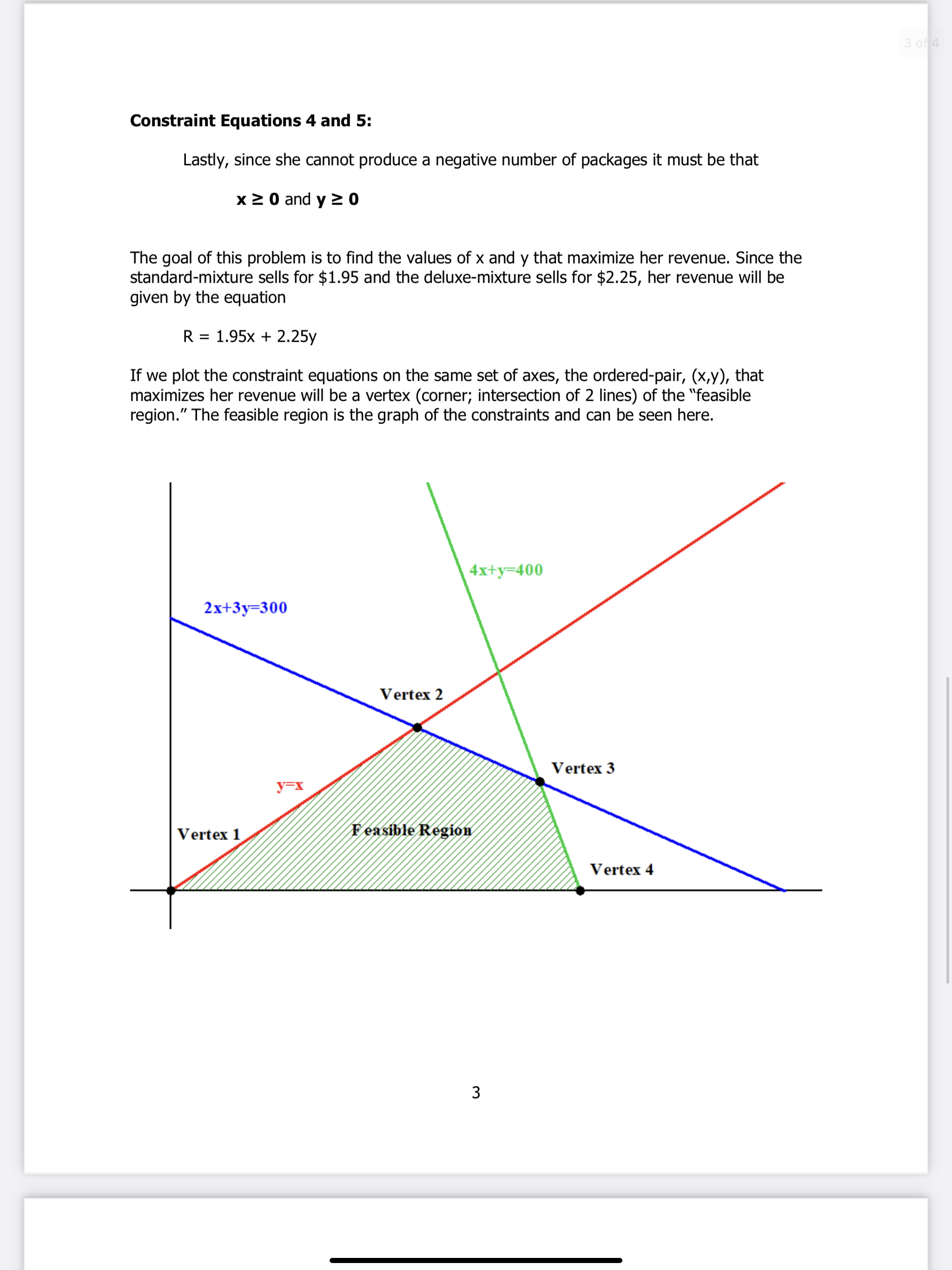
Constraint Equations 4 and 5: Lastly, since she cannot produce a negative number of packages it must be that x a 0 and y a 0 The goal of this problem is to nd the values of x and y that maximize her revenue. Since the standard-mixture sells for $1.95 and the deluxe-mixture sells for $2.25, her revenue will be given by the equation R = 1.95x + 2.25y If we plot the constraint equations on the same set of axes, the ordered-pair, (x,y), that maximizes her revenue will be a vertex (corner; intersection of 2 lines) of the \"feasible region.\" The feasible region is the graph of the constraints and can be seen here. 2x+3y=300 Part 1 Exercises: 1. Find the coordinates of the vertices of the feasible region. Clearly show how the vertex is determined and which lines form the vertex. a. Find the coordinates of vertex 1. b. Find the coordinates of vertex 2. c. Find the coordinates of vertex 3. d. Find the coordinates of vertex 4. 2. Find the value of R for each vertex. a. Calculate R for vertex 1. b. Calculate R for vertex 2. c. Calculate R for vertex 3. d. Calculate R for vertex 4. 3. How many standard-mixture packages and how many deluxe-mixture packages should she sell to maximize her revenue? Part 2: Linear Programming Problem 2 Consider the feasible region in the xy-plane dened by the following linear inequalities. x20 yZO x510 x+y25 x+2ys 18 Part 2 Exercises: 1. Find the coordinates of the vertices of the feasible region. Clearly show how each vertex is determined and which lines form the vertex. 2. What is the maximum and the minimum value of the function Q = 60x+78y on the feasible region