Part 3 (50 marks)

Write the Excel formula for each cell marked with ?? in column B

of figure 1, and label each formula clearly.

List all the constraints in terms of the cell positions in figure 1.

A construction company has been contracted by a major league football team to build a new football stadium with a car parking lot. The teams current stadium was built for both baseball and football, and it has an enclosed oval shape, with seating around the entire circumference. Football crowds can fill the stadium to full capacity, but baseball games only fill the stadium to 70% of the total capacity. Thus the new stadium will be for football games only.

It is decided that the new stadium will be U-shaped, like a horseshoe. Seating would be all around the U, but there would be no seat at the open end. The construction engineers have calculated the length around the U (leaving out the open end part) as 1375 feet, and plan to build 100 rows of seats that extend back and up from the playing field. In fact, the geometry of the stadium is such that the row closest to the playing field (1st row) is shorter in length than the row farthest from the playing field (100th row). However, some of those rows are broken by equipments, exits, and concessions. Thus to simplify calculations for this study, you can assume that each of the 100 rows in the new stadium is 1375 feet in length. The construction engineers plan to install four kinds of seats:

Box seats are the rows of seats closest to the playing field and are usually considered the most desirable and expensive.

Red seats are the rows of seats in the next level up.

Blue seats are the rows of seats in the level above the red seats.

Yellow seats are the farthest rows up and away from the playing field, and they are

the least desirable and cheapest.

The construction company needs to know the optimal number of seats for each type of seats to build in the new football stadium so that the total revenue would be maximized in the forecast plan, which is done in a Microsoft Excel spreadsheet using Excels Solver. You are required to quantify the financial impacts of different stadium construction alternatives by writing Excel formulae and constraints to help with the calculations of this problem see the spreadsheet (in figure 1 below). Microsoft Excels Solver will calculate the number of seats to be built in cells B4 to B7 (changing cells) for each kind of seat.

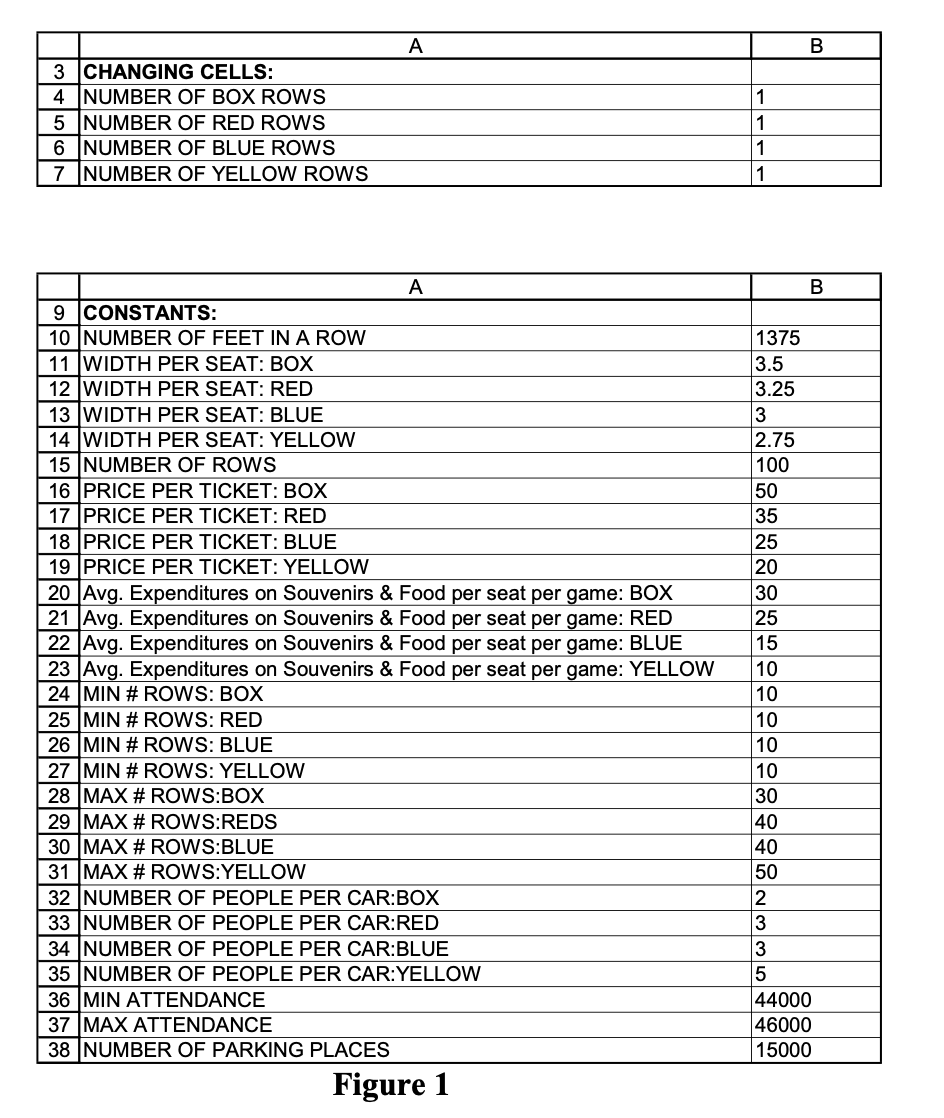
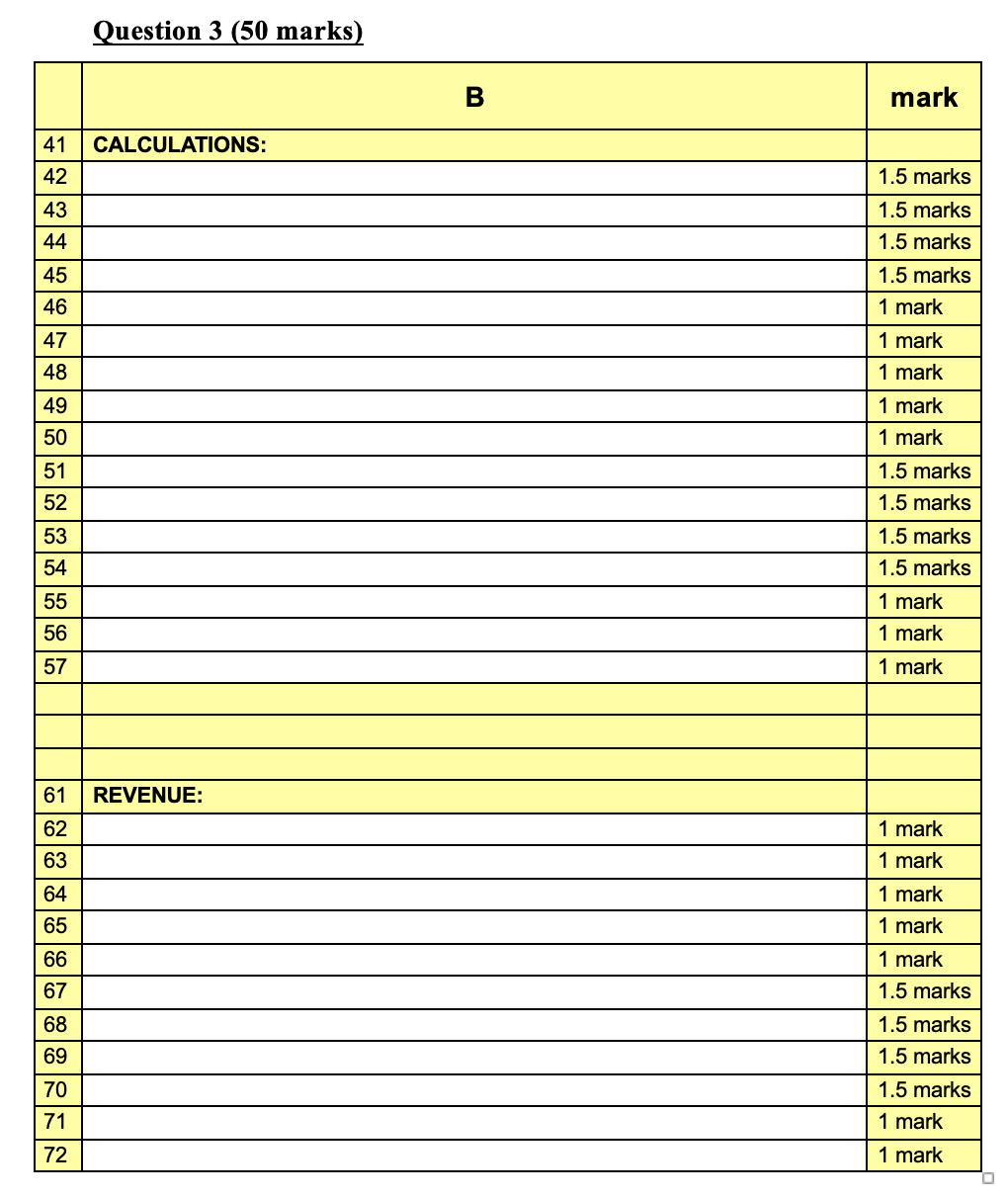
\begin{tabular}{|c|l|l|} \hline & \multicolumn{1}{|c|}{ A } & \multicolumn{1}{c|}{B} \\ \hline 3 & CHANGING CELLS: & \\ \hline 4 & NUMBER OF BOX ROWS & 1 \\ \hline 5 & NUMBER OF RED ROWS & 1 \\ \hline 6 & NUMBER OF BLUE ROWS & 1 \\ \hline 7 & NUMBER OF YELLOW ROWS & 1 \\ \hline \end{tabular} \begin{tabular}{|c|l|l|} \hline & \multicolumn{1}{|c|}{ A } & \multicolumn{1}{c|}{B} \\ \hline 9 & CONSTANTS: & \\ \hline 10 & NUMBER OF FEET IN A ROW & 1375 \\ \hline 11 & WIDTH PER SEAT: BOX & 3.5 \\ \hline 12 & WIDTH PER SEAT: RED & 3.25 \\ \hline 13 & WIDTH PER SEAT: BLUE & 3 \\ \hline 14 & WIDTH PER SEAT: YELLOW & 2.75 \\ \hline 15 & NUMBER OF ROWS & 100 \\ \hline 16 & PRICE PER TICKET: BOX & 50 \\ \hline 17 & PRICE PER TICKET: RED & 35 \\ \hline 18 & PRICE PER TICKET: BLUE & 25 \\ \hline 19 & PRICE PER TICKET: YELLOW & 20 \\ \hline 20 & Avg. Expenditures on Souvenirs \& Food per seat per game: BOX & 30 \\ \hline 21 & Avg. Expenditures on Souvenirs \& Food per seat per game: RED & 25 \\ \hline 22 & Avg. Expenditures on Souvenirs \& Food per seat per game: BLUE & 15 \\ \hline 23 & Avg. Expenditures on Souvenirs \& Food per seat per game: YELLOW & 10 \\ \hline 24 & MIN \# ROWS: BOX & 10 \\ \hline 25 & MIN \# ROWS: RED & 10 \\ \hline 26 & MIN \# ROWS: BLUE & 10 \\ \hline 27 & MIN \# ROWS: YELLOW & 10 \\ \hline 28 & MAX \# ROWS:BOX & 30 \\ \hline 29 & MAX \# ROWS:REDS & 40 \\ \hline 30 & MAX\# \#OWS:BLUE & 40 \\ \hline 31 & MAX\# ROWS:YELLOW & 50 \\ \hline 32 & NUMBER OF PEOPLE PER CAR:BOX & 2 \\ \hline 33 & NUMBER OF PEOPLE PER CAR:RED & 3 \\ \hline 34 & NUMBER OF PEOPLE PER CAR:BLUE & 3 \\ \hline 35 & NUMBER OF PEOPLE PER CAR:YELLOW & 5 \\ \hline 36 & MIN ATTENDANCE & 44000 \\ \hline 37 & MAX ATTENDANCE & 46000 \\ \hline 38 & NUMBER OF PARKING PLACES & 15000 \\ \hline \end{tabular} Figure 1 Figure 1 - continued The "Constants" section of the spreadsheet (see cells A9 to cells B38) contains the following data: - The average length of a row of seats is 1375 feet (cell B10). - The total number of rows in the stadium is 100 (cell B15). - Major football league rules state that the stadium must have a minimum number of 44000 seats (cell B36). - The team management has set a maximum of 46000 (cell B37) for the total number of seats. - The seat types differ by more than just paint colour and their positions in the stadium. The most expensive seats will be the widest and therefore, the most comfortable. The least expensive seats will be the narrowest and therefore, the least comfortable. This means the number of seats in a Box seat row will be fewer than the number of seats in a Red seat row and so on. The width of seats and the admission ticket price for each seat type are shown in below table: - People who come to watch ballgames usually buy souvenirs and food. In fact, many fans spend more money on food and souvenirs than they do on their admission tickets. The team's research department has determined that there is a correlation between where fans sit and how much they spend on souvenirs and food. The table below shows the average expenditures by each seat type per game: - The new stadium will need a parking lot that can accommodate 15000 cars (cell B38). The team's researchers have studied how fans get to the stadium. They have found that the less-affluent fans are more likely to use public transportation rather than drive a car to the game. Their research reveals the following averages: * For every 2 fans sitting in Box seats (cell B32), 1 car arrives at the stadium. * For every 3 fans sitting in Red seats (cell B33), 1 car arrives at the stadium. * For every 3 fans sitting in Blue seats (cell B34), 1 car arrives at the stadium. * For every 5 fans sitting in Yellow seats (cell B35), 1 car arrives at the stadium. - The team management would like a balance among the different seating types. The minimum and maximum number of rows for each kind of seat is shown in below table: The "Calculations" section of the spreadsheet (see cell A41 to cell B72) contains immediate results that will be used in the income statement of the spreadsheet, and/or will be used as constraints. Write Excel formulae for the following: - Number of seats per row for each seat type - Box, Red, Blue, Yellow (cells B42 to cell B45) is a function of the length of the row and of the width of seats in each row. Since a fraction of a seat can't be built, the number of seats per row for each seat type must be a whole number, thus leaving some spare space in each row of seats. - Total number of seats in each seat type - Box, Red, Blue, Yellow (cells B46 to B49) is a function of the number of seats per row for each seat type and the number of rows for each seat type. - The total number of seats for all seat types (cell B50) in the stadium. - The number of cars arriving at the stadium for a match for each seat type - Box, Red, Blue, Yellow (cells B51 to B54) is the function of the number of fans per car for each seat type and the number of seats for each seat type. Since a fraction of a car does not exist, the number of cars for each seat type must be a whole number, thus leaving some spare space in the parking lot. - Total number of cars arriving at the stadium for a match for all seat types (cell B55). - Total number of rows to be installed in the stadium (cell B56). - Total number of rows to be installed for Red and Blue seats (cell B57). The "Revenue" section of the spreadsheet (see cell A61 to cell B72) contains the "total revenue" that the Solver is expected to maximize. Write Excel formulae for the following: - Total ticket sales revenue for each seat type - Box, Red, Blue, Yellow (cells B62 to B65) is a function of the ticket price for each seat and the number of seats for each seat type. - Total revenue from all tickets of all seat types (cell B66). - Total revenue gained from selling food and souvenirs for each seat type - Box, Red, Blue, Yellow (cell B67 to B70). - Total revenue gained from selling food and souvenirs for all seat types (cell B71). - Total revenue from ticket sales and from selling food and souvenirs for all seat types (cell B72). Constraints part (Each constraint is worth 1 mark): The team management's goal is to maximize the total revenue subject to various constraints, with the assumption that all seats' admission tickets will be sold for each match. Formulate constraints from the following statements that are made by the team's management: The total number of rows in the stadium must be 100 (cell B15). Major football league rules state that the stadium must have a minimum number of 44000 seats (cell B36). However, team management wants the stadium to appear "intimate", so it is decided that the stadium should not be able to seat more than 46000 fans (cell B37). The team management does not want the new stadium to have a massive "cheap seats" area. Thus it is decided that the number of rows of Red seats plus the number of rows of Blue seats combined, must be greater than or equal to the number of rows of Yellow seats. For the car parking lot, it is decided that more space should be allocated to the seating area, and thus the car parking lot should accommodate at most 15,000 cars (cell B38). The team management would also like a balance among the different seating types. The minimum and maximum number of rows for each kind of seat are shown in below table: Finally, fractional part for the number of rows for each seat type is not allowed, as this is an integer problem. Question 3 (50 marks) Constraints: there are 18 constraints. \begin{tabular}{|c|l|l|} \hline & \multicolumn{1}{|c|}{ A } & \multicolumn{1}{c|}{B} \\ \hline 3 & CHANGING CELLS: & \\ \hline 4 & NUMBER OF BOX ROWS & 1 \\ \hline 5 & NUMBER OF RED ROWS & 1 \\ \hline 6 & NUMBER OF BLUE ROWS & 1 \\ \hline 7 & NUMBER OF YELLOW ROWS & 1 \\ \hline \end{tabular} \begin{tabular}{|c|l|l|} \hline & \multicolumn{1}{|c|}{ A } & \multicolumn{1}{c|}{B} \\ \hline 9 & CONSTANTS: & \\ \hline 10 & NUMBER OF FEET IN A ROW & 1375 \\ \hline 11 & WIDTH PER SEAT: BOX & 3.5 \\ \hline 12 & WIDTH PER SEAT: RED & 3.25 \\ \hline 13 & WIDTH PER SEAT: BLUE & 3 \\ \hline 14 & WIDTH PER SEAT: YELLOW & 2.75 \\ \hline 15 & NUMBER OF ROWS & 100 \\ \hline 16 & PRICE PER TICKET: BOX & 50 \\ \hline 17 & PRICE PER TICKET: RED & 35 \\ \hline 18 & PRICE PER TICKET: BLUE & 25 \\ \hline 19 & PRICE PER TICKET: YELLOW & 20 \\ \hline 20 & Avg. Expenditures on Souvenirs \& Food per seat per game: BOX & 30 \\ \hline 21 & Avg. Expenditures on Souvenirs \& Food per seat per game: RED & 25 \\ \hline 22 & Avg. Expenditures on Souvenirs \& Food per seat per game: BLUE & 15 \\ \hline 23 & Avg. Expenditures on Souvenirs \& Food per seat per game: YELLOW & 10 \\ \hline 24 & MIN \# ROWS: BOX & 10 \\ \hline 25 & MIN \# ROWS: RED & 10 \\ \hline 26 & MIN \# ROWS: BLUE & 10 \\ \hline 27 & MIN \# ROWS: YELLOW & 10 \\ \hline 28 & MAX \# ROWS:BOX & 30 \\ \hline 29 & MAX \# ROWS:REDS & 40 \\ \hline 30 & MAX\# \#OWS:BLUE & 40 \\ \hline 31 & MAX\# ROWS:YELLOW & 50 \\ \hline 32 & NUMBER OF PEOPLE PER CAR:BOX & 2 \\ \hline 33 & NUMBER OF PEOPLE PER CAR:RED & 3 \\ \hline 34 & NUMBER OF PEOPLE PER CAR:BLUE & 3 \\ \hline 35 & NUMBER OF PEOPLE PER CAR:YELLOW & 5 \\ \hline 36 & MIN ATTENDANCE & 44000 \\ \hline 37 & MAX ATTENDANCE & 46000 \\ \hline 38 & NUMBER OF PARKING PLACES & 15000 \\ \hline \end{tabular} Figure 1 Figure 1 - continued The "Constants" section of the spreadsheet (see cells A9 to cells B38) contains the following data: - The average length of a row of seats is 1375 feet (cell B10). - The total number of rows in the stadium is 100 (cell B15). - Major football league rules state that the stadium must have a minimum number of 44000 seats (cell B36). - The team management has set a maximum of 46000 (cell B37) for the total number of seats. - The seat types differ by more than just paint colour and their positions in the stadium. The most expensive seats will be the widest and therefore, the most comfortable. The least expensive seats will be the narrowest and therefore, the least comfortable. This means the number of seats in a Box seat row will be fewer than the number of seats in a Red seat row and so on. The width of seats and the admission ticket price for each seat type are shown in below table: - People who come to watch ballgames usually buy souvenirs and food. In fact, many fans spend more money on food and souvenirs than they do on their admission tickets. The team's research department has determined that there is a correlation between where fans sit and how much they spend on souvenirs and food. The table below shows the average expenditures by each seat type per game: - The new stadium will need a parking lot that can accommodate 15000 cars (cell B38). The team's researchers have studied how fans get to the stadium. They have found that the less-affluent fans are more likely to use public transportation rather than drive a car to the game. Their research reveals the following averages: * For every 2 fans sitting in Box seats (cell B32), 1 car arrives at the stadium. * For every 3 fans sitting in Red seats (cell B33), 1 car arrives at the stadium. * For every 3 fans sitting in Blue seats (cell B34), 1 car arrives at the stadium. * For every 5 fans sitting in Yellow seats (cell B35), 1 car arrives at the stadium. - The team management would like a balance among the different seating types. The minimum and maximum number of rows for each kind of seat is shown in below table: The "Calculations" section of the spreadsheet (see cell A41 to cell B72) contains immediate results that will be used in the income statement of the spreadsheet, and/or will be used as constraints. Write Excel formulae for the following: - Number of seats per row for each seat type - Box, Red, Blue, Yellow (cells B42 to cell B45) is a function of the length of the row and of the width of seats in each row. Since a fraction of a seat can't be built, the number of seats per row for each seat type must be a whole number, thus leaving some spare space in each row of seats. - Total number of seats in each seat type - Box, Red, Blue, Yellow (cells B46 to B49) is a function of the number of seats per row for each seat type and the number of rows for each seat type. - The total number of seats for all seat types (cell B50) in the stadium. - The number of cars arriving at the stadium for a match for each seat type - Box, Red, Blue, Yellow (cells B51 to B54) is the function of the number of fans per car for each seat type and the number of seats for each seat type. Since a fraction of a car does not exist, the number of cars for each seat type must be a whole number, thus leaving some spare space in the parking lot. - Total number of cars arriving at the stadium for a match for all seat types (cell B55). - Total number of rows to be installed in the stadium (cell B56). - Total number of rows to be installed for Red and Blue seats (cell B57). The "Revenue" section of the spreadsheet (see cell A61 to cell B72) contains the "total revenue" that the Solver is expected to maximize. Write Excel formulae for the following: - Total ticket sales revenue for each seat type - Box, Red, Blue, Yellow (cells B62 to B65) is a function of the ticket price for each seat and the number of seats for each seat type. - Total revenue from all tickets of all seat types (cell B66). - Total revenue gained from selling food and souvenirs for each seat type - Box, Red, Blue, Yellow (cell B67 to B70). - Total revenue gained from selling food and souvenirs for all seat types (cell B71). - Total revenue from ticket sales and from selling food and souvenirs for all seat types (cell B72). Constraints part (Each constraint is worth 1 mark): The team management's goal is to maximize the total revenue subject to various constraints, with the assumption that all seats' admission tickets will be sold for each match. Formulate constraints from the following statements that are made by the team's management: The total number of rows in the stadium must be 100 (cell B15). Major football league rules state that the stadium must have a minimum number of 44000 seats (cell B36). However, team management wants the stadium to appear "intimate", so it is decided that the stadium should not be able to seat more than 46000 fans (cell B37). The team management does not want the new stadium to have a massive "cheap seats" area. Thus it is decided that the number of rows of Red seats plus the number of rows of Blue seats combined, must be greater than or equal to the number of rows of Yellow seats. For the car parking lot, it is decided that more space should be allocated to the seating area, and thus the car parking lot should accommodate at most 15,000 cars (cell B38). The team management would also like a balance among the different seating types. The minimum and maximum number of rows for each kind of seat are shown in below table: Finally, fractional part for the number of rows for each seat type is not allowed, as this is an integer problem. Question 3 (50 marks) Constraints: there are 18 constraints