Part $3$: Regularization

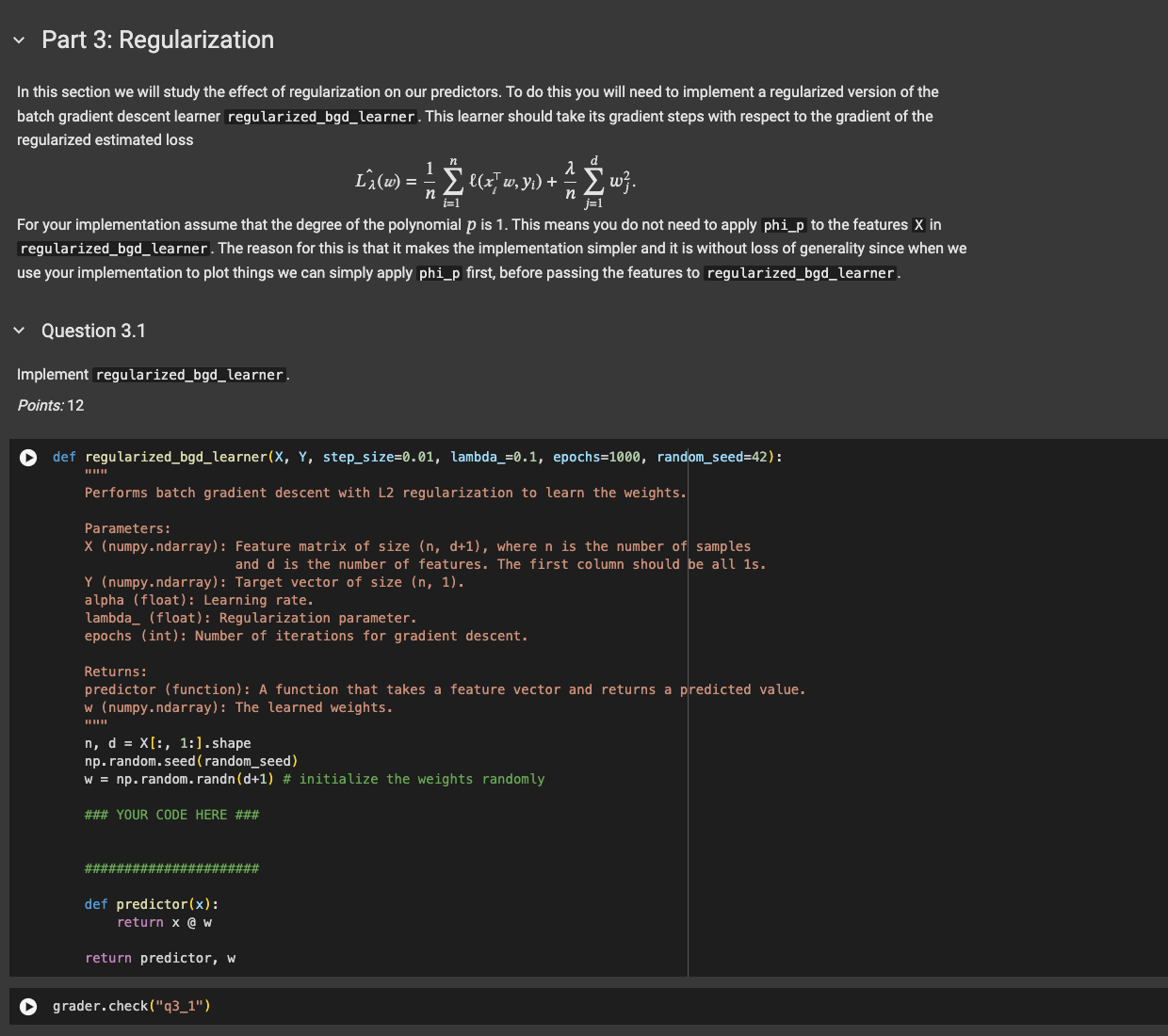
In this section we will study the effect of regularization on our predictors. To do this you will need to implement a regularized version of the batch gradient descent learner regularized$\_$bgd$\_$learner. This learner should take its gradient steps with respect to the gradient of the regularized estimated loss

$\backslash [$

$\backslash$hat$\{$L$\_\{\backslash$lambda$\}\}($w$)=\backslash$frac$\{1\}\{$n$\}\backslash$sum$\_\{$i$=1\}^\{$n$\}\backslash$ell$\backslash$left$($x$\_\{$i$\}^\{\backslash$top$\}$ w$,$ y$\_\{$i$\}\backslash$right$)+\backslash$frac$\{\backslash$lambda$\}\{$n$\}\backslash$sum$\_\{$j$=1\}^\{$d$\}$ w$\_\{$j$\}^\{2\}.$

$\backslash ]$

For your implementation assume that the degree of the polynomial $\backslash ($ p $\backslash )$ is $1.$ This means you do not need to apply phi$\_$p to the features $\backslash (\backslash$mathbf$\{$X$\}\backslash )$ in regularized$\_$bgd$\_$learner. The reason for this is that it makes the implementation simpler and it is without loss of generality since when we use your implementation to plot things we can simply apply phi$\_$p first, before passing the features to regularized$\_$bgd$\_$learner.

Question $3\mathrm{.}1$

Implement regularized$\_$bgd$\_$learner.

Points: $12$

$```$

def regularized$\_$bgd$\_$learner$($X$,$ Y$,$ step$\_$size$=0\mathrm{.}01,$ lambda$\_=0\mathrm{.}1,$ epochs$=1000,$ random$\_$seed$=42)$:

$"!"$

Performs batch gradient descent with L$2$ regularization to learn the weights.

Parameters:

X $($numpy$.$ndarray$)$: Feature matrix of size $($n$,$ d$+1),$ where n is the number of samples

and d is the number of features. The first column should be all $1$s$.$

Y $($numpy$.$ndarray$)$: Target vector of size $($n$,1).$

alpha $($float$)$: Learning rate.

lambda$\_($float$)$: Regularization parameter.

epochs $($int$)$: Number of iterations for gradient descent.

Returns:

predictor $($function$)$: A function that takes a feature vector and returns a predicted value.

w $($numpy$.$ndarray$)$: The learned weights.

$"\text{'}""$

n$,$ d $=$ X$[$:$,1$:$].$shape

np$.$random.seed$($random$\_$seed$)$

w $=$ np$.$random.randn$($d$+1)$ # initialize the weights randomly

### YOUR CODE HERE ###

######################

def predictor$($x$)$:

return x @ w

return predictor, w

$```$