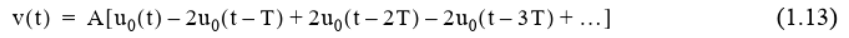
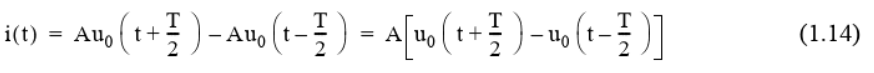
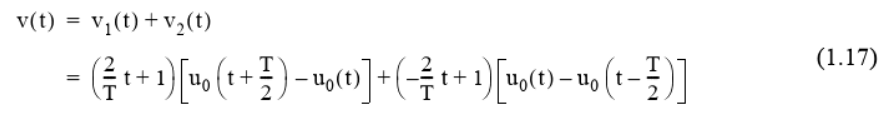
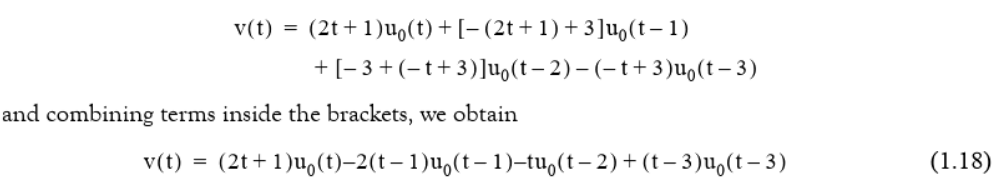
Part 3 Use the heaviside and ezplot functions to validate equations 1.13, 1.14, 1.17 and 1.18 in the textbook (Karris 2012). The Ramp Function The integral of the unit step function is the ramp function u(t) = = [ uo(t)dt Gives Fot 0 = tuo(t) To verify this result: syms tau ul(t)= int(heaviside(tau), -inf, t) Plot the ramp function ezplot(u1(t), [-1,5]), grid title('u_1(t)') v(t) A[uo(t) 2uo(t T)+2uo(t 2T) 2uo(t 3T)+...] (1.13) i(t) Auo (t+1 ) - Aug (t) = A[uo(t + ) -uo(t-1)] (1.14) v(t) = vy(t) + v2(t) (1.17) +(e+1)[vo (t+1) -1,0))+(1+1)(wo(0) uo(t-1)] v(t) (2t + 1)uo(t)+(-(2+1) +3]uo(t-1) + [-3+(-t+3)]u,(t2)-(-t+3)u(t-3) and combining terms inside the brackets, we obtain v(t) (2t+1)u,(t)-2(t-1)u,(t-1)-tu,(t 2)+(t 3)u,(t-3) (1.18) Part 3 Use the heaviside and ezplot functions to validate equations 1.13, 1.14, 1.17 and 1.18 in the textbook (Karris 2012). The Ramp Function The integral of the unit step function is the ramp function u(t) = = [ uo(t)dt Gives Fot 0 = tuo(t) To verify this result: syms tau ul(t)= int(heaviside(tau), -inf, t) Plot the ramp function ezplot(u1(t), [-1,5]), grid title('u_1(t)') v(t) A[uo(t) 2uo(t T)+2uo(t 2T) 2uo(t 3T)+...] (1.13) i(t) Auo (t+1 ) - Aug (t) = A[uo(t + ) -uo(t-1)] (1.14) v(t) = vy(t) + v2(t) (1.17) +(e+1)[vo (t+1) -1,0))+(1+1)(wo(0) uo(t-1)] v(t) (2t + 1)uo(t)+(-(2+1) +3]uo(t-1) + [-3+(-t+3)]u,(t2)-(-t+3)u(t-3) and combining terms inside the brackets, we obtain v(t) (2t+1)u,(t)-2(t-1)u,(t-1)-tu,(t 2)+(t 3)u,(t-3) (1.18)