Part A - Automata Construction

1.Draw a DFA which accepts the following language over the alphabet of {0,1}: the set of all strings which contain a block of four consecutive symbols exactly two of which are 0. Your DFA must handle all intput strings in {0,1}*. Here is a methodical way to do this:

Figure out all the final states and label each with the shortest string it accepts,

work backwards from these states to the starting state, labelling each state you create with the shortest string accepted so far,

add the missing transitions.

The labelling of the states with the shortest string it accepts is important in order to not get confused.

2.Draw a DFA which accepts the following language over the alphabet of {0,1}: the set of all strings such that each any block of four consecutive symbols does not have exactly two 1's. Your DFA must handle all intput strings in {0,1}*. (Hint: look at solution of previous question) Note: "each" has been changed to "any" because people were finding "each" ambiguous.

3.Draw the simplest possible (i.e. with fewest number of states) NFA which accepts the following language over the alphabet of {a, e, i, o, u, b, p, r, s, t}: the set of strings which start with a consonant, then one or more vowels, then a consonant, and after reading any sequence of 0 or more symbols from the alphabet, eventually ends with the same vowel that preceded the second consonant.

4.Assuming that you have the following three automata, A₁, A₂, A₃ recognizing the languages L₁, L₂, L₃ respectively, shown here as black boxes:

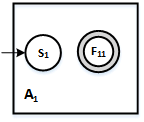
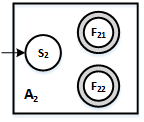
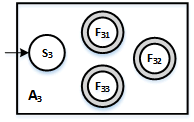
a. Draw an NFA called A which recognizes the language L₂ L₁ (L₁* | L₃)

b. What is the starting state of A?

c. What are A's final states?

S1 F1 S1 F1