Question: part a eqn is provided. Z should be lambda b and c please MAA2(zf2zi2)=RTDABPln[(PpA(sat))P]t A measuring cylinder of height L is initially three quarters full
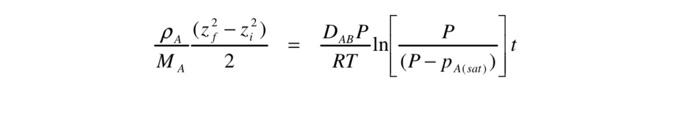
![c please MAA2(zf2zi2)=RTDABPln[(PpA(sat))P]t A measuring cylinder of height L is initially three](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/09/66f8d65610510_82966f8d6559323a.jpg)
MAA2(zf2zi2)=RTDABPln[(PpA(sat))P]t A measuring cylinder of height L is initially three quarters full of water. Over time, evaporation of liquid causes the liquid level in the cylinder to fall. It can be assumed that the evaporation rate is controlled by diffusion of water vapour with diffusivity DA, diffusion being considered to take place through stagnant air from the surface of the water to the top of the cylinder, the air at the top of the cylinder being perfectly dry. Likewise it can be assumed that the air has pressure p, temperature T and that water has vapour pressure pv at temperature T. Liquid water can be assumed to have a molar mass M and density 1. a) Suppose that at some arbitrary point in time t, the liquid level is some distance t below the top of the cylinder. Obtain an expression (in terms of t ) for the instantaneous flux of water vapour NA under these circumstances. b) Determine how t varies as a function of time t, remembering that initially (at time t=0 ), the cylinder is three quarters full. c) Suppose that at a particular time t=t1/2, the cylinder is half full. Using the expression derived above for t versus t, obtain an explicit expression for t1/2
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


