Part A: (The Concepts): True/False (12 marks):Answer each question given below by answering if the question is true or false.In the textbox given, include your explanation for your choice.Each question is worth two marks: one mark for the explanation and one mark for the correct answer.

1.The value of the derivative at a point on a function measures the slope of the tangent to the curve at that point.

2.The acceleration function is found by differentiating the displacement function twice.

3.The quotient rule can be used to differentiate a rational function.

4.The derivative of a polynomial function is always another polynomial function.

5.The sign, positive or negative, of the velocity of an object at a specific time indicates the direction in which the object is moving.

6.An object is slowing down when the acceleration of the object is in the opposite direction of its motion.

Part B (Using the Concepts): Multiple Choice:(28 marks)Each question is worth different marks according to the strategy used.If calculations are required, the mark for the strategy will worth more marks and the final answer will be worth one mark.

Identify the choice that best completes the statement or answers the question.Your choices are given below the text box.Make sure you include your strategy.

7.Find if f'(1) if f(x)= 3x^2+x+1 .(two marks)

a. 3

b. 6

c. 7

d. 8

8.Find f'(1)if f(x)= (x^3)^2 .(two marks)

a. -6

b. -5

c. 6

d. 5

9.Find f'(3) if

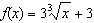
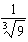
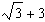
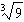
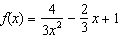
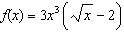
\f\f\f\f\f\f