Part B

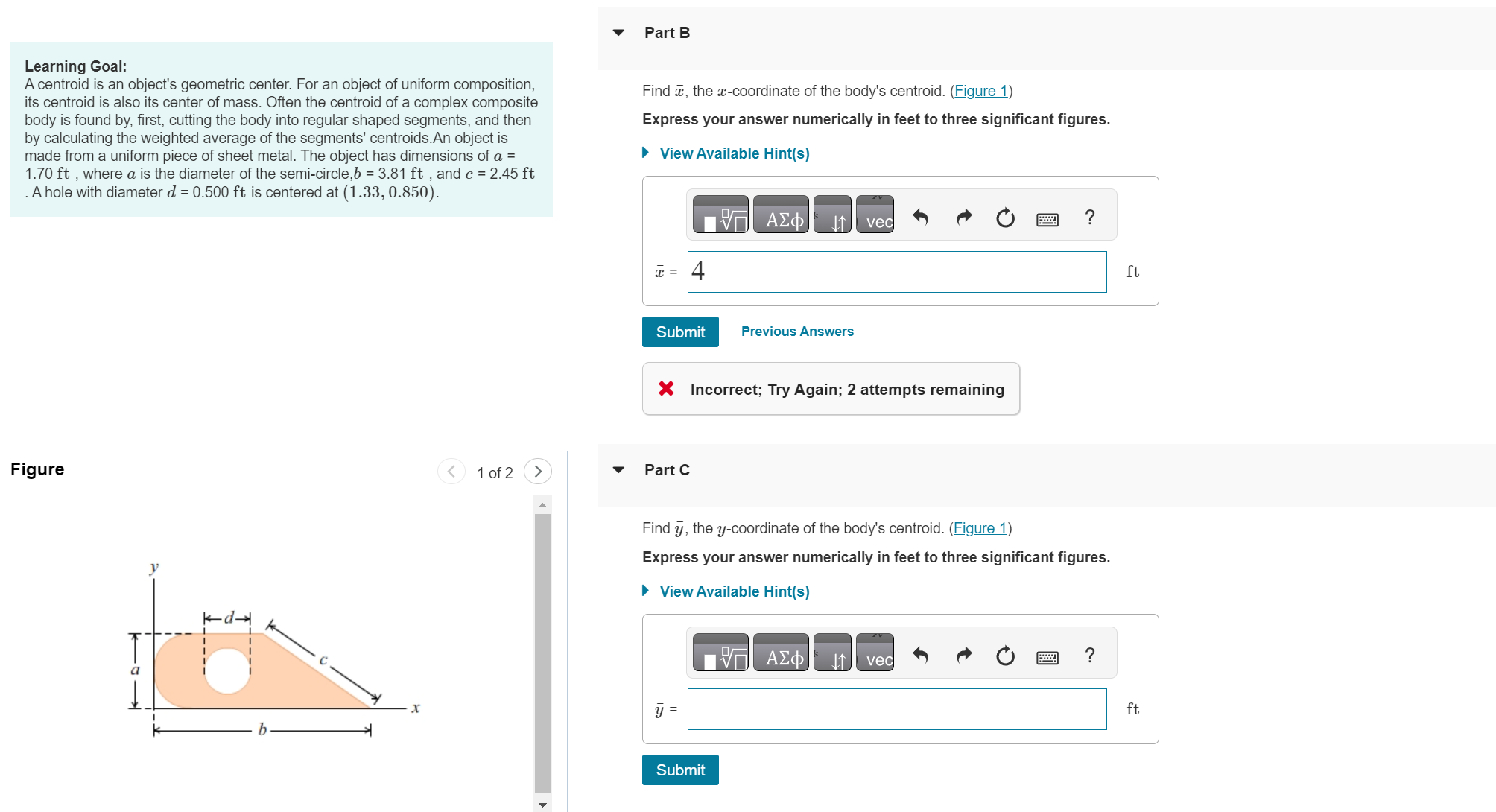
Learning Goal:

A centroid is an object's geometric center. For an object of uniform composition, its centroid is also its center of mass. Often the centroid of a complex composite body is found by$,$ first, cutting the body into regular shaped segments, and then by calculating the weighted average of the segments' centroids. An object is made from a uniform piece of sheet metal. The object has dimensions of $\backslash ($ a$=\backslash )1\mathrm{.}70$ ft $,$ where $\backslash ($ a $\backslash )$ is the diameter of the semi$-$circle, $\backslash ($ b$=3\mathrm{.}81\backslash$mathrm$\{$ft$\}\backslash ),$ and $\backslash ($ c$=2\mathrm{.}45\backslash$mathrm$\{$ft$\}\backslash ).$ A hole with diameter $\backslash ($ d$=0\mathrm{.}500\backslash$mathrm$\{$ft$\}\backslash )$ is centered at $\backslash ((1\mathrm{.}33,0\mathrm{.}850)\backslash ).$

Figure

$1$ of $2$

Find $\backslash (\backslash$bar$\{$x$\}\backslash ),$ the $\backslash ($ x $\backslash )-$coordinate of the body's centroid. $($Figure $1)$

Express your answer numerically in feet to three significant figures.

$-$ View Available Hint$($s$)$

Previous Answers

Incorrect; Try Again; $2$ attempts remaining

Part C

Find $\backslash (\backslash$bar$\{$y$\}\backslash ),$ the $\backslash ($ y $\backslash )-$coordinate of the body's centroid. $($Figure $1)$

Express your answer numerically in feet to three significant figures.

View Available Hint$($s$)$

$\backslash (\backslash$bar$\{$y$\}=\backslash )$

ft Learning Goal:

A centroid is an object's geometric center. For an object of uniform composition, its centroid is also its center of mass. Often the centroid of a complex composite body is found by$,$ first, cutting the body into regular shaped segments, and then by calculating the weighted average of the segments' centroids.An object is made from a uniform piece of sheet metal. The object has dimensions of $\backslash ($ a$=\backslash )1\mathrm{.}70$ ft $,$ where $\backslash ($ a $\backslash )$ is the diameter of the semi$-$circle, $\backslash ($ b$=3\mathrm{.}81\backslash$mathrm$\{$ft$\}\backslash ),$ and $\backslash ($ c$=2\mathrm{.}45\backslash$mathrm$\{$ft$\}\backslash ).$ A hole with diameter $\backslash ($ d$=0\mathrm{.}500\backslash$mathrm$\{$ft$\}\backslash )$ is centered at $\backslash ((1\mathrm{.}33,0\mathrm{.}850)\backslash ).$

Figure

$-$ View Available Hint$($s$)$

Part D

A single$-$scoop ice cream cone is a composite body made from a single scoop of ice cream placed into a cone. $($Figure $2)$ Assume that the scoop of ice cream is a sphere with radius $\backslash ($ r$=1\mathrm{.}46\backslash$mathrm$\{$in$\}\backslash )$ that is placed into a $4\mathrm{.}00$ in tall cone. The interior height of the cone is $3\mathrm{.}60$ in$.$ The cone has an exterior radius of $1\mathrm{.}25$ in and an interior radius of $1\mathrm{.}10$ in$.$ The scoop of ice cream sits on the cone's interior radius and extends into the cone some distance. Find the $\backslash (\backslash$bar$\{$z$\}\backslash )$ centroid for the cone $($the scoop of ice cream and the cone$).$

Express your answer numerically in inches to three significant figures.

$-$ View Available Hint$($s$)$

Part E Complete previous part$($s$)$

Part F Complete previous part$($s$)$

Provide Feedback