Part B. MATLAB*********************************

The answer output needs to be in the following format:

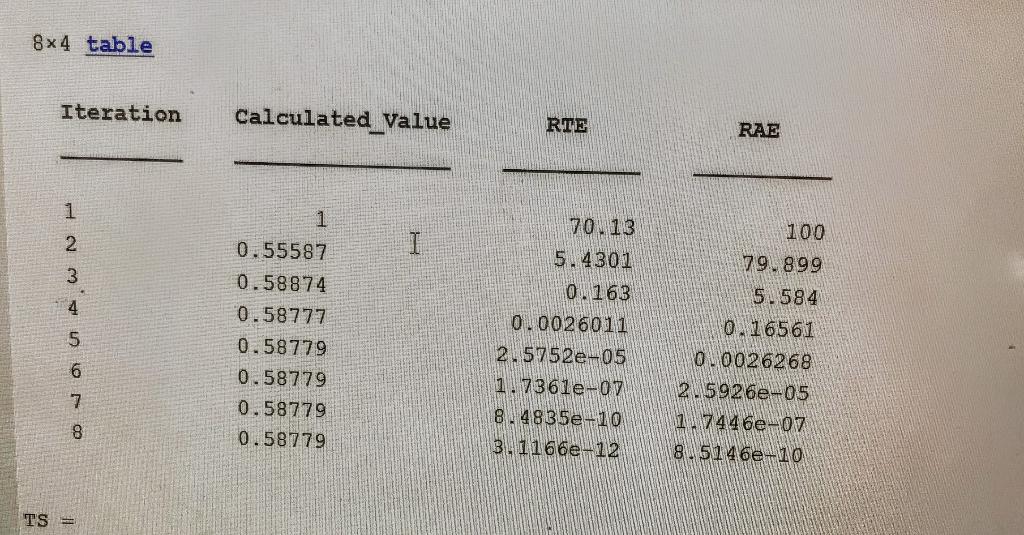
a. 14. Determine the number of terms necessary to approximate cos x to 8 significant figures using Maclaurin series approximation. r cosx = 1 + 2 4! 6! 8! Calculate and display the approximation using a value of x = 0.31. Do this by hand using 4 terms to evaluate cos x. Compute relative true error (%) and relative approximate error (%) as terms are added. Create a table that shows the iteration number, calculated value of cos x, relative true error (that you can calculate based on the built-in cosine function in your calculator or Excel) and relative approximate error. b. Write a MATLAB function to evaluate the series. The code should allow an infinite number of terms, but should be used to evaluate the series to 8 significant figures. The code should also be able to run until it reaches either a maximum number of iterations (specified by the user) or a stopping criterion (such as a minimum relative approximate error, specified by the user in %). Include default values of maxit (=100) in the event that they are not specified by the user. Output a table that shows the iteration number, calculated value of cos x, relative true error (that you can calculate based on the built-in cosine function) and relative approximate error. 8x4 table Iteration Calculated_Value RIE RAE 1 1 I coonWN 0.55587 0.58874 0.58777 0.58779 0.58779 0.58779 0.58779 70 13 5.4301 10 163 0.0026011 2.5752e-05 1 7361e-07 8.4835e-10 3.1166e_12 100 79.899 5.584 0.16561 0.0026268 2 5926e-05 1.7446e-07 85146e-10 TS = a. 14. Determine the number of terms necessary to approximate cos x to 8 significant figures using Maclaurin series approximation. r cosx = 1 + 2 4! 6! 8! Calculate and display the approximation using a value of x = 0.31. Do this by hand using 4 terms to evaluate cos x. Compute relative true error (%) and relative approximate error (%) as terms are added. Create a table that shows the iteration number, calculated value of cos x, relative true error (that you can calculate based on the built-in cosine function in your calculator or Excel) and relative approximate error. b. Write a MATLAB function to evaluate the series. The code should allow an infinite number of terms, but should be used to evaluate the series to 8 significant figures. The code should also be able to run until it reaches either a maximum number of iterations (specified by the user) or a stopping criterion (such as a minimum relative approximate error, specified by the user in %). Include default values of maxit (=100) in the event that they are not specified by the user. Output a table that shows the iteration number, calculated value of cos x, relative true error (that you can calculate based on the built-in cosine function) and relative approximate error. 8x4 table Iteration Calculated_Value RIE RAE 1 1 I coonWN 0.55587 0.58874 0.58777 0.58779 0.58779 0.58779 0.58779 70 13 5.4301 10 163 0.0026011 2.5752e-05 1 7361e-07 8.4835e-10 3.1166e_12 100 79.899 5.584 0.16561 0.0026268 2 5926e-05 1.7446e-07 85146e-10 TS =