Part b

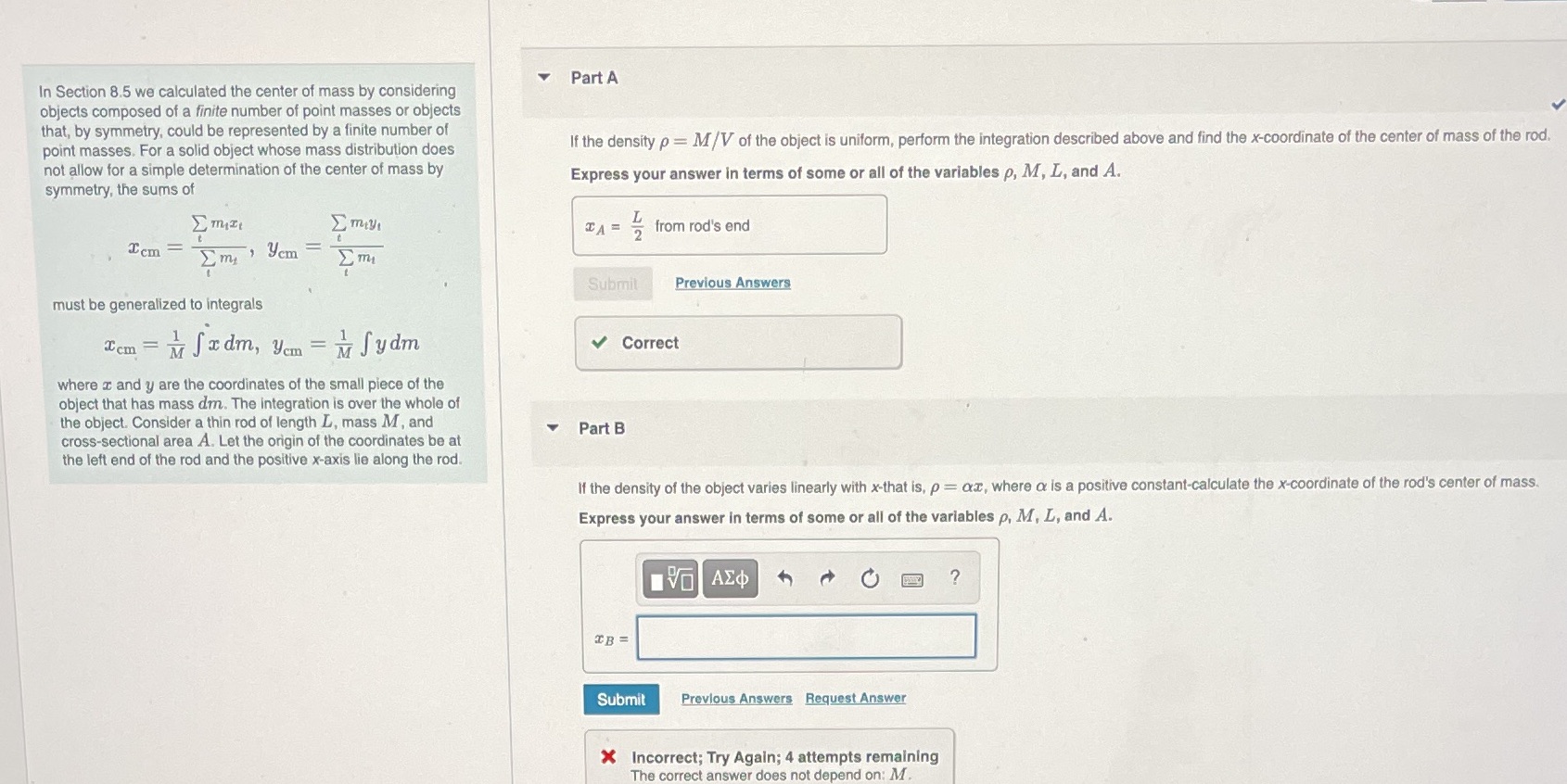
Part A In Section 8.5 we calculated the center of mass by considering objects composed of a finite number of point masses or objects that, by symmetry, could be represented by a finite number of point masses. For a solid object whose mass distribution does If the density p = M/V of the object is uniform, perform the integration described above and find the x-coordinate of the center of mass of the rod. not allow for a simple determination of the center of mass by Express your answer in terms of some or all of the variables p, M, L, and A. symmetry, the sums of Emty 2 from rod's end Cem = yem Submit Previous Answers must be generalized to integrals Tem = M Jxdm, yom = M Sydm Correct where r and y are the coordinates of the small piece of the object that has mass dm. The integration is over the whole of the object. Consider a thin rod of length L, mass M, and Part B cross-sectional area A. Let the origin of the coordinates be at the left end of the rod and the positive x-axis lie along the rod. If the density of the object varies linearly with x-that is, p = QI, where o is a positive constant-calculate the x-coordinate of the rod's center of mass. Express your answer in terms of some or all of the variables p, M, L, and A. IVO AED 4 0 0 0 ? TBE Submit Previous Answers Request Answer Incorrect; Try Again; 4 attempts remaining The correct answer does not depend on: M