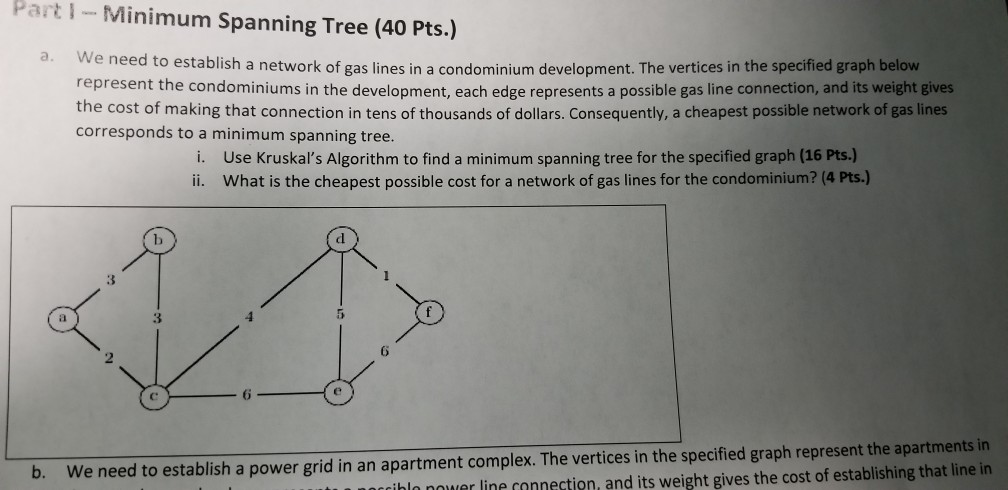
Part i Minimum Spanning Tree (40 Pts.) a. W e need to establish a network of gas lines in a condominium development. The vertices in the specified graph below represent the condominiums in the development, each edge represents a possible gas line connection, and its weight gives the cost of making that connection in tens of thousands of dollars. Consequently, a cheapest possible network of gas lines corresponds to a minimum spanning tree. i. Use Kruskal's Algorithm to find a minimum spanning tree for the specified graph (16 Pts.) i. What is the cheapest possible cost for a network of gas lines for the condominium? (4 Pts.) 3 6 6 We need to establish a power grid in an apartment complex. The vertices in the specified graph represent the apartments in lo nower line rnnection, and its weight gives the cost of establishing that line in b