PARTICIPATION

ACTIVITY

$3\mathrm{.}1\mathrm{.}6$: Proof: Two Boolean expressions are equivalent $1.$

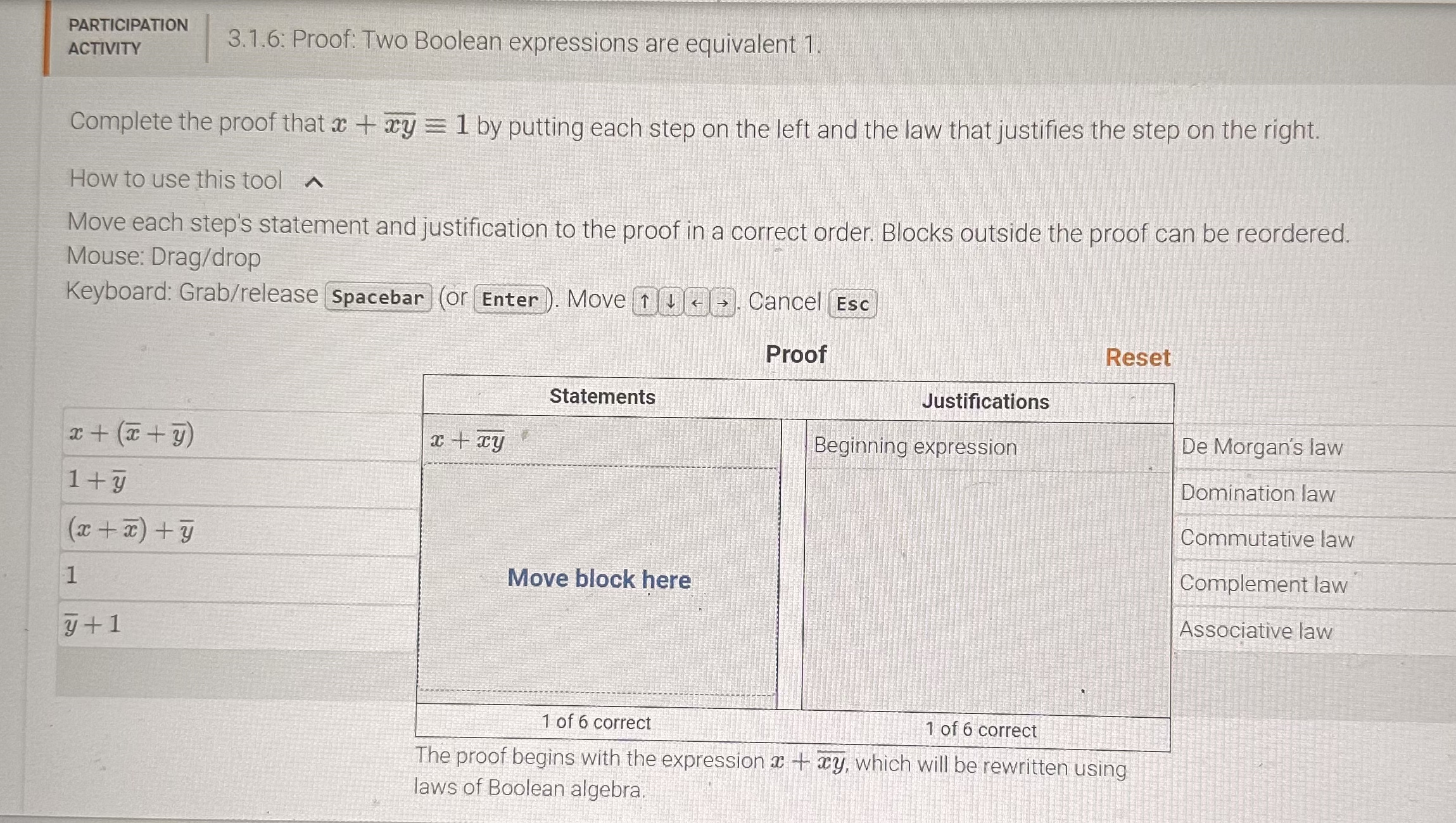
Complete the proof that $x\frac{+}{b}ar(xy)-=1$ by putting each step on the left and the law that justifies the step on the right.

How to use this tool

Move each step's statement and justification to the proof in a correct order. Blocks outside the proof can be reordered.

Mouse: Drag$/$drop

Keyboard: Grab$/$release Spacebar $($or Enter$).$ Move uarrdarrlarr$.$ Cancel Esc

Proof

Reset

$\backslash$table$[[x+(\stackrel{}{x}\frac{+}{b}ar(y)),$Statements$],[1\frac{+}{b}ar(y),x\frac{+}{b}ar(xy),],[(x+\stackrel{}{x})\frac{+}{b}ar(y),$Justifications,$],[1,$Move block here,$],[\frac{?}{\text{b}\text{a}\text{r}}(y)+1,,]]$

De Morgan's law

Domination law

Commutative law

Complement law

Associative law

The proof begins with the expression $x\frac{+}{b}ar(xy),$ which will be rewritten using laws of Boolean algebra.