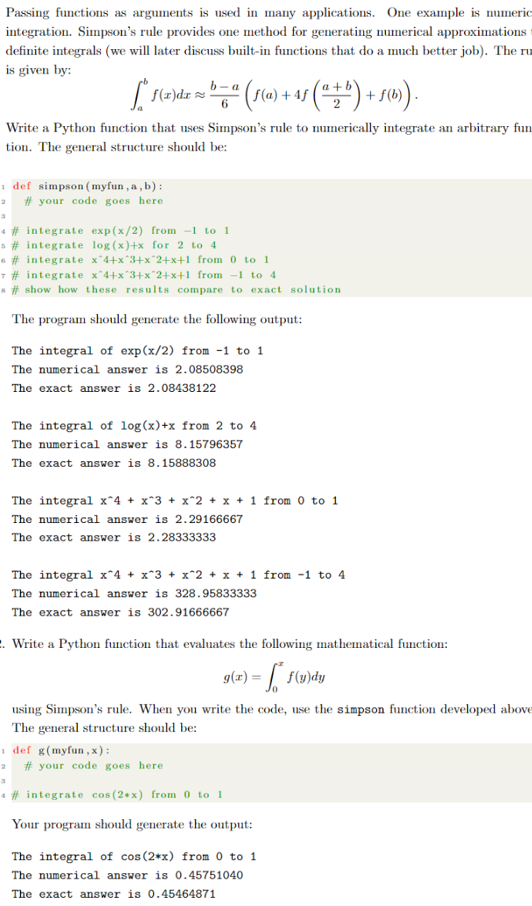
Passing functions as arguments is used in many applications. One example is numeric integration. Simpson's rule provides one method for generating numerical approximations definite integrals (we will later discuss built-in functions that do a much better job). The is given by: abf(x)dx6ba(f(a)+4f(2a+b)+f(b)). Write a Python function that uses Simpson's rule to numerically integrate an arbitrary fun tion. The general structure should be: The program should generate the following output: The integral of exp(x/2) from 1 to 1 The numerical answer is 2.08508398 The exact answer is 2.08438122 The integral of log(x)+x from 2 to 4 The numerical answer is 8.15796357 The exact answer is 8.15888308 The integral x4+x3+x2+x+1 from 0 to 1 The numerical answer is 2.29166667 The exact answer is 2.28333333 The integral x4+x3+x2+x+1 from 1 to 4 The numerical answer is 328.95833333 The exact answer is 302.91666667 Write a Python function that evaluates the following mathematical function: g(x)=0xf(y)dy using Simpson's rule. When you write the code, use the simpson function developed above The general structure should be: def g(myfun,x) : \# your code goes here \# integrate cos(2x) from 0 to 1 Your program should generate the output: The integral of cos(2x) from 0 to 1 The numerical answer is 0.45751040 The exact answer is 0.45464871