Physics Lab Question (Projectile motion)

Part 1 : Protocol / Instructions (Including specific formulas during different stages of the marble)

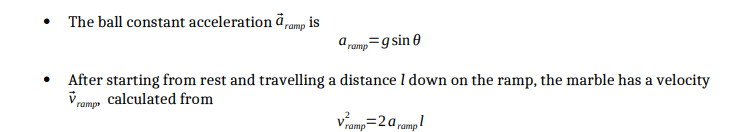
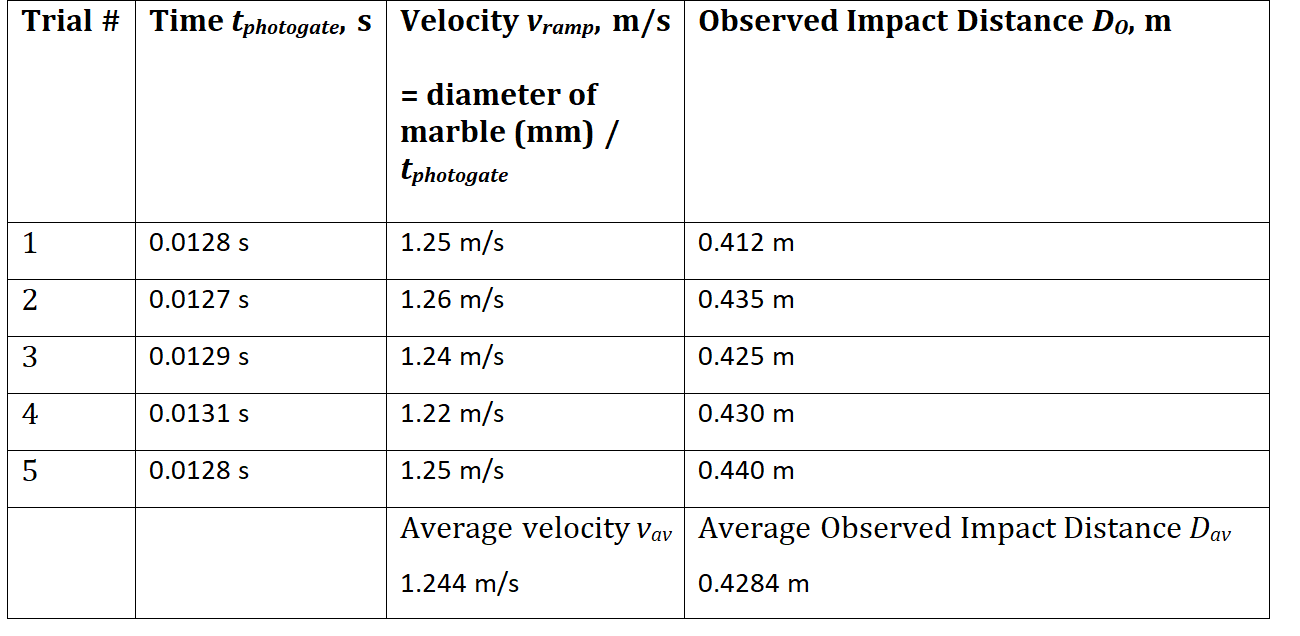
PURPOSE Investigate projectile motion and linear motion on a ramp. . Calculate the final velocity at the end of a ramp Predict the impact point of the projectile after it falls a specific vertical distance. . Compare observations for projectile motion and calculations to determine sources of error. EQUIPMENT Marble, track (ramp), photogate, Vernier caliper, meter stick, tape, target sheet, plumb bob (string and washer BACKGROUND In this lab activity, you will predict and then measure the horizontal impact distance D of a projectile launched from an elevated position. In order to measure the horizontal distance that the projectile travels upon rolling of a table, you need to know its initial horizontal velocity as well as the time it is in the air. The projectile is a glass marble that rolls down from rest on a ramp with a length I then transition on the horizontal table top, so that it leaves the table with a horizontal velocity. Since the velocity of the projectile as it leaves the table has no vertical component, the time it is in the air before it hits the ground is calculated based on the height H of the table. Table Top projectile Path Plumb Line H D Fig. 1 from "Energy of a Rolling Object", University of North Carolina, https://www.webassign.net/question_assets/unccolphysmechl1/lab_6/manual.html Linear Motion on a Ramp For the marble constrained to accelerate down the ramp at an angle with the horizontal, both the acceleration and velocity vectors are parallel to the ramp. On the coordinate system with the x-axis along the ramp and the y-axis perpendicular, the ball has an accelerated motion along the x-axis.. The ball constant acceleration @ramp is ramp= g sin 0 After starting from rest and travelling a distance I down on the ramp, the marble has a velocity Vramp calculated from V ramp=2 C ramp IWhen the ball reaches the end of the ramp, it continues in projectile motion with the velocity Vramp (vo in the figure above) as its initial velocity. The projectile motion is a combination of a uniform motion on the x axis and free fall on the y axis. Horizontal D = V ramp flight v =V ramp = constant Vertical 2H 2 H=-g t night SO t flight= 1 g V=g t night V + 1 PROCEDURE 1. Measure the diameter d of the marble with the Vernier caliper.2. Measure with the meter stick the distance I of 40.0 cm from the bottom of the ramp up and mark it with a pen or a piece of tape as the marble's starting point on the ramp. 3. Release the marble from the starting point and allow it to roll off the table to approximate the spot on the ground where it lands. 4. Measure the height h of the ramp, from the starting point vertically down to the table. 5. Use the sine ratio to find the angle @ the ramp makes with the horizontal. 0=sin-12 6. Calculate the theoretical velocity van the marble should have when leaving the ramp Vi=2 ramp /=2 gl sin 0 7. Tape a piece of string to the edge of the table so the string hangs vertically from the table, then tie the washer to the bottom end of the string; this plumb line allows you to find the point on the floor directly below the point where the marble leaves the table. Ramp Plumb Bob Floor Origin Fig. 3 from Go Direct@ Photogate User Manual, Vernier.com, https://www.vernier.com/manuals/gdx-vpg/ 8. Measure with the metre stick the height H from the top of the table to the floor; follow the plumb line to make sure the metre stick is straight. 9. Calculate 2 H t flight = g 10. Use tnight to calculate Don, the Theoretical Impact Distance, the marble should travel horizontally from the end of the table to the landing point on the floor. DMV th t flight 11. Measure from floor origin directly beneath the plumb line the distance Do, in the same direction with the ramp, then place the target paper on the floor at that point. 12. Set up the photogate at the edge of the table, 3 cm from the lower end of the ramp so that the marble passes between the arms of the photogate before it leaves the table. Photo Gate Steel Ball "plumb Bob" Ramp 313. Release the marble; it will roll down the ramp, across the table, then off the table to land on the target sheet; marl: the location of its landing on the target sheet 14. Record the time IWNUEJW the marble passes through the photogate. o Instructions on how to operate the photogates are provided with each photogate set 15. Measure the distance on the oor from the landing point to the point directlyr below the end of the table. Record the distance as Du, the Observed Impact Distance. 16. Repeat this process 4 more times, making sure to release the marble from the same position on the ramp. Record each interval time tpamagm and observed impact distance Do in Table 1. Title the table. 1?. Calculate the actual velocity the marble has when leaving the table v : at t romp phumgute 18. Determine the average v\" for the ve calculated values for v.1\". 1'9. Calculate the relative error for v, considering vs. the true value and v.Iv the measured value. measured value true value 2% X lD 'i-i': true value relative error 2D. Determine the average D\" for the ve measured D0. 2 1. Calculate the relative error for the horizontal distance Um pact Distance] the marble traveled before hitting the oor, using Dl'h as the true value and Day as the measured value. Discuss possible sources of error. Motion in a Plane - Part I + toppr Motion in a plane Examples of motion in two dimensions. Circular motion Projectile motion Equations of motion in a straight line Equations of motion in a plane vau+ at Apply equations of motion in a straight line separately in both directions, X and Y. s= ut + ! at V, = U. + a,t Vy =U, + a,t v = u' + 2as v = final velocity of the particle S, = u,t +! a,t? sy = ut + at u = initial velocity of the particle s = displacement of the particle v', = u', + 2a,s vy = u'y+ 2a,5 a = acceleration of the particle t = the time interval in which the particle is in consideration Projectile motion . Projectile refers to an object that is in flight along the horizontal and vertical direction simultaneously. . Acceleration acts only in the vertical direction due to acceleration due to gravity (g). . No acceleration in the horizontal direction. usin 0 B . Projectile motion is always in the form of parabola. u cos 0 g y = ax + bx g soon V C Formulas for projectile motion Components of velocity at time t u, = u cose u, = u sine-gt Position at time t x = (u cos0)t y = (u sin0)t - 1/2 gt Equation of path of projectile motion y = (tan 0)x - gx?/2(u cose)2 Time of maximum height tm = u sine /g Time of flight 2tm = 2(u sine/g) Maximum height of projectile hm = (u sine)?/2g Horizontal range of projectile R = u' sin 20/g Maximum horizontal range ( 0. = 45 ) Rm = u'/gDiameter of the marble d [mm] 16 mm Height of the ramp h [mm] 105.4 mm Length of the ramp I [mm] 365 mm Height of table H [mm] 740 mm Calculated angle 0 the ramp makes with the horizontal 170 Trial # Time tphotogate, S Velocity Vramp, m/S| Observed Impact Distance Do, m = diameter of marble (mm) / tphotogate 0.0128 s 1.25 m/s 0.412 m 2 0.0127 s 1.26 m/s 0.435 m 3 0.0129 s 1.24 m/s 0.425 m 4 0.0131 s 1.22 m/s 0.430 m 5 0.0128 s 1.25 m/s 0.440 m Average velocity Vav | Average Observed Impact Distance Dav 1.244 m/s 0.4284 mQuestion 1: Using the length and height of the ramp, calculate the theoretical velocity 1% the marble should have when leaving the ramp [magnitude and angle]. Question 2 : Compare the theoretical velocity Pm calculated in the previous question with the average velocity val; of the marble determined in Table 1. Question 3 Use measured height of table H to calculate the time the projectile is in the air, tight. Question 4 Use , tight and the theoretical velocity vth to calculations for Dan the Theoretical Impact Distance the marble travelled from the end of the table to the floor where it hits the ground. Question 5 Calculate the relative error for the horizontal distance [Impact Distance] the marble traveled before hitting the floor, by using Dth as the true value and DW as the measured value. Question 6 Discuss possible sources of error for Dth and vm. Question 7 Use a ruler and a protractor to draw a scaled diagram showing the theoretical path of the marble. Label on your diagram the height and the length of the ramp, the height of the table, and the theoretical impact distance. Question 8 Using your data, calculate the velocity of the marble at impact. Your answer must include the magnitude and angle. Draw a vector representing this velocity on your diagram for the previous